Unusual Gobans
| Table of contents | Table of diagrams Irregular goban roundgo equivalent (81 points) diagonal liberties 4D Go Board Black's chain. Layer 1 Layer 2 |
Go can be played on virtually any surface, provided it's flat enough. It has been played on maps of the world, among other things. For all these games, the normal rules apply. To see which odd gobans you can create at SL and how, see Creating Irregular Gobans With Wiki. Some programs are named at the bottom of this page.
Non-square Rectangular Gobans
The simplest of these is a rectangular goban, see 13x9 for an example game.
Gobans smaller than 2x3 typically lead to a game which ends with repetitive captures or superko, respectively, hence the outcome becomes highly dependent on the ruleset used.
Physically Irregular Gobans
Other possibilities lie in the creation of gobans which are irregular.
The simplest one of these is basically a normal goban, with a hole in the middle, but of course you can make a goban in any shape you wish, and the lines connecting the intersections need not necessarily be straight, equal length or even at straight angles to each other. However, gobans like these are normally made more for fun than to play serious games on.
For a game on a goban with no tengen, see Virtueless. See also Coin Go.
This is an example made in the sandbox
Giant's Causeway Goban
I guess this fits into the category above. An outwardly normal looking goban, Constructed from 400 individual pieces of wood, there are only two known examples of this board. It has featured in the side events of the 2004/2005 Irish Open. The board is turned upside down, whereupon it has a 3-D undulating topology. In 2005 the traditional game of VertiGo was played on it, dropping stones from a height onto the board. The first man to capture one or more stones wins.
Found an image of this goban: 
Fewer Borders
Edgeless Go
Finite graphs where all points have four liberties may or may not be locally grid-like. Explanations and analysis of this distinction are in the page on edgeless Go.
RoundGo and Relatives
![[ext]](images/extlink.gif) This one looks cool.
It's hard to describe, but every intersection has 4 liberties (even the edges). On it a sensei lost to a 2 kyu.
--SifuEric
This one looks cool.
It's hard to describe, but every intersection has 4 liberties (even the edges). On it a sensei lost to a 2 kyu.
--SifuEric
rubilia: The round go provided by the link above is equivalent to a half-borderless, half-borderlined diagonal (4+5)x9 board:
Just imagine this ...
... with the stubs along the long edges bent flat and connected to form a continous line at both sides (that's the "borderlines", which correspond to the outer and the inner circle of roundgo), while the short edges are simply joined by the stubs so that their "border" points become adjacent (that's the "borderless" border). If the long edges were joined, too, the game would become a rectangular 9x9 borderless like described as Toroidal Board below.
MortenPahle: Btw, this diagram is exactly what you get by matching together side by side the two disparate parts of Sebastian's diagonal board analysis, given below.I think of it as being a 'squashed' cylinder (hence I put it at 3DOn2DGoban) - you can imagine it being stretched around the outside (or inside :-) of a cylinder - the number of intersections for each 'ring' is the same...
starline: I've got that pattern hanging up in my bedroom! It's called a 'dream-catcher' and it's made out of string inside a circular frame. It has feathers hanging from the bottom of it (the whole thing is tied by string to a beam, and it moves gently in the air currents). I haven't tried playing go on it yet :)
Zarlan: Does it chatch dreams about Go? ;)
starline: Zarlan, I don't know if it's caught any go dreams lately, as I haven't emptied it for a while ^^.
jvloenen: At the club we used to play "Kolder Go" (Humbug Go ?) once a year. Nine years ago we played "normal rules, unusual boards". The circular board happened to be the most interesting. (I lost a game by starting a ladder, well, don't!).
I created printed boards to be used with normal sized stones. The boards are made up by plain postscript, and will fit on A3 paper. Every A3-PostScript capable printer should print the boards fine. GhostScript? will do too of course. If you like to try, you can find the source ![[ext]](images/extlink.gif) here. The text is dutch (sorry). You will find the links to the PostScript-source left to the diagrams.
here. The text is dutch (sorry). You will find the links to the PostScript-source left to the diagrams.
Toroidal Board
See toroidal Go.
Lattices
Recently, I've found a comprehensive web site about go at various lattices: http://www.leipzig-go.de/gitter/index_e.html (sorry, link dead).
Ed Cherlin: The oddest go layout I have heard of was a 3-dimensional diamond crystal lattice. You can see a picture of a very small part of the structure at ![[ext]](images/extlink.gif) http://cst-www.nrl.navy.mil/lattice/struk/a4.html (dead link). Each point is connected to four others at the vertices of a regular tetrahedron. Ladders are helical, and there are very strange edge effects. This 'board' was written up in an English-language Go magazine in the 1960s.
http://cst-www.nrl.navy.mil/lattice/struk/a4.html (dead link). Each point is connected to four others at the vertices of a regular tetrahedron. Ladders are helical, and there are very strange edge effects. This 'board' was written up in an English-language Go magazine in the 1960s.
![[ext]](images/extlink.gif) Henry Segerman has built a wire "Diamond Go" with every intersection having 4 liberties. It is played with pieces made out of paper or cardboard.
Henry Segerman has built a wire "Diamond Go" with every intersection having 4 liberties. It is played with pieces made out of paper or cardboard.
Gobans with any number of corners and liberties
See at the bottom of this page under "Programs" for Wastl Sommer's Java applet.
Maps
- From a post to RGG by Matthew MACFADYEN
[...] A good one was a map of Switzerland, constructed in 1984 by Patrice GOSTELI. Here there were 361 intersections with numbers of liberties varying from 1 to about 15. Features included:
- Zurich
- poorly connected to the rest of the board but with two adjacent points having only it as liberties, so a play there (banker) had two eyes instantly.
- Porrentruy
- the venue for that year's European Championship, had about 15 liberties many of which were on the edge.
- The mountains
- an area where most points had 2 or 3 liberties. very hard to make eyes, full of surprising liberty shortage problems. It was possible to surround the whole mountain area with a surprisingly small number of stones.
- The plains
- a flat area where most points had 6 liberties, normally ended up as dame.
- Liechtenstein
- four intersections not connected to the rest of the board - a 4 point endgame play.
Other possibilities lie in playing on regular boards where the points are not connected as squares. Hexagonal connections (chinese checkers layout) can be played on, as can of course any combination of triangles, squares, pentagons, etc. etc.
- TimHunt:
![[ext]](images/extlink.gif) Milton Keynes Go is another example of a goban based on a map, in this case a map of the English town of Milton Keynes. It is approximately a square grid, but with rather irregular edges and a few points with only three liberties in the middle of the board. Unfortunately, I don't think that the diagramming facilities of Senseis Library are good enough for me to give you a picture! You'll just have to follow the link above.
Milton Keynes Go is another example of a goban based on a map, in this case a map of the English town of Milton Keynes. It is approximately a square grid, but with rather irregular edges and a few points with only three liberties in the middle of the board. Unfortunately, I don't think that the diagramming facilities of Senseis Library are good enough for me to give you a picture! You'll just have to follow the link above.
-
![[ext]](images/extlink.gif) Go Waterloo is a map that represents the positions and movement of units during the Battle of Waterloo. The game fails to fulfill any promise of giving fans of Waterloo board games historical accuracy in troop movement and often it's unclear if White or Black is Napoleon until the end of the game.
Go Waterloo is a map that represents the positions and movement of units during the Battle of Waterloo. The game fails to fulfill any promise of giving fans of Waterloo board games historical accuracy in troop movement and often it's unclear if White or Black is Napoleon until the end of the game.
Other Lattices
- Another interesting idea I have toyed with is the concept of playing go on Celtic Knots. You could play anywhere that two lines intersected, and a point's liberties would be the next 4 intersections reached by following the knot out in all 4 directions from that point. The result would be that some points would have liberties quite far away. If you allow play on corners (which occur differently in celtic knots than in grids) then all points would have 4 liberties, except the corners themselves which would have 2. Alternatively, if you do not allow play on corners, then some points would have 3 and 2 liberties. The way in which celtic knots are constructed would allow you to create boards in any shape, with interesting factors, such as permanent walls partway down the middle, or entire sections of the board connected to the rest by only one point. Because of the amazing diversity of celtic knots, and how easy it is to construct them, it would allow lots of variety. Take a look at
![[ext]](images/extlink.gif) http://www.wallace.net/knots/samples/ and see what I mean.
http://www.wallace.net/knots/samples/ and see what I mean.
Other Ideas
Partially Severed Connections
axd: A generalisation of the Milton Keynes variant is to partially sever connections. So three types of connections can exist between two neighbouring points 'A' and 'B': the full (classical) connection, a half connection extending from A or no connection. The interesting case is the half connection: it provides a liberty for point 'A' from which it departs, but not for its neighbouring point 'B', where it does not arrive. So, playing on 'B' takes away a liberty from 'A', but 'A' never influences 'B'. This introduces a concept of "rough (or high) terrain" in the game. Jurgen Ott's GoWin screensaver "barrier" setting partially reflects this idea by completely cutting out some intersections. The standard Goishi size will give a big practical problem: partial connections are almost impossible to see below the stones.
doraguma: see also NetGo rules
Rotated Board
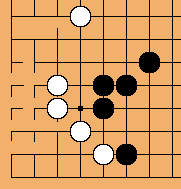
A non-square goban can be made by turning a normal board 45 degrees, and using the new definitions of horizontal and vertical to define liberties. That is:
In this diagram, the black stone has just been captured. The marked white stone has four free liberties, each marked with a square.
This goban has a few unusual features:
- Each corner has only one liberty.
- Every intersection on the edge has only two liberties.
- The edges are not directly connected.
- No intersection has exactly three liberties.
- Playing on this board is like playing two, simultaneous games. If two pieces would be next to each other on a normal goban, on a diagonal goban, they do not interact.
(Sebastian:) So what's the point? Why make the game artificially confusing?
ChipUni: It's an unusual goban that requires nothing more than what go players already have.
(Sebastian:) Well, yes, all unusual boards add some form of a challenge. But let me explain what I mean: Your change can be separated in a functional and a graphical component.
Functionally, your goban is equivalent to this:
[123]
The graphical change is tantamount to (a) rotating them, (b) enmeshing them and (c) changing the lines so that they connect stones from different half-boards rather than adjacent stones. While this change does create an inconveniency which you may regard as a challenge, it certainly does not introduce any new way of playing, tactics or strategy.
As to the functional change, it actually takes away from the desirable complexity of go. Splitting the board into two disparate half-boards only destroys many interesting strategic connections. If you are willing to play for a certain amount of time in one chunk, why not just play on one board that's twice as big?
ihope?: one way to make the boards interact is to make the stones larger so that connected stones actually touch. This prevents placing stones horizontally or vertically adjacent to each other. This does add some interesting new plays.
minostrel?:This variant presented here, basically use rotated von neumann neighborhood (where chess bishop can go when moving only one square) to find who are the neighbors instead of normal go that use von neumann neighborhood (where chess rook can go when moving just one square). With rotated von neumann neighborhood, some pieces won't touch others, similar to whatt happens with chess, where a bishop can't capture a piece at opposite color no matter the amount of moves you have to do it.
To remove (or at least reduce) the "two half boards" problem, you can use edgeless boards. Imagine a M x N sized board, now imagine that if a board is E x E, it means both axies are even sized, if it is O X O it means both axies are odd sized, and if as some example an board is Ew X EW, this means both axies are even sized and both axies wrap around. The boards that would not be colorbound are EW X OW, OW X EW, EW X E, OW X E, OW X O, E X EW, E X OW, O X OW. All those boards allow groups that are part of both "half boards"
3D and 4D Goban
CJ I regularly play on 3D boards and have made a 4D one too! The 3D boards are 4*4*4 ie 4 boards of 4*4 in a stack just like 3d tic-tac-toe. Most points have 6 liberties, the corners only 3, and the games are mostly about making life in 3D for one or mabie two clusters. Each side can usualy make only 3 or 4 moku, if they manage life at all...
The 4D one is slightly trickier to explain... if anyone can fix my boards that would be a great help, I need to separate the middle into 4 4*4 boards, and can't get rid of the little errors
uxs:Fixed the errors by replacing underscores with dashes. As for the line you want, where do you want it? Couldn't you just use 4 separate boards?
cj: Thanks for the fixes (doh!), I tried making 4 separate boards (that is what the real one I use has) but it seems to spread them out too much. I'll leave them as one of each, unless anyone (uxs?) has any better ideas
uxs: It looks fine like this. Maybe it would be a good idea to number the stones on the board with the black chain, so you can see more easily which stones are connected each other.
To understand how the board works, see it as 2 separate 4*4*4 boards, one running top left to bottom right and the other top right to bottom left:
A 1 A is above B is above C is above D B 2 and 3 C 1 is above 2 is above 3 is above 4 4 D
So far so good? Now the fun (4th dimensional) part: The middle four boards naturaly resemble an 8*8 board, so it makes sense to play it as an 8*8 board also. this means a piece on the bottom right corner of 'B board' would be next to the bottom left corner of '2' whilst at the same time being above a piece in the bottom right of 'C' (by 'normal' 3D connection). Here is an example where all black pieces form an unbroken chain:
The central plane made by the 4 middle board has many interesting properties, with opposite corners above/below eachother and also next to eachother (via the other two boards). These connections make it impossible to manufacture in a 3 dimensional space, but quite simple in a 4d one, hence the claim of 4D go.
The power of the central plane makes control of the middle paramount in the 4d game, with control of 1/4 of the middle immediatly scoring 16 moku since the board that connects to that 1/4 is secure (ie controling all of B means the opponent can't play on A, since there are no eyes possible, and al of your pieces have life automaticaly). However controling B is difficult if you opponent plays on C or the edges of 2 or 3 makeing the start of the game very complex!
Have fun with these mind-twisting creations, and if you are in Edinburgh look me up for a game on the worlds first 4D go board ;)
- CJ
uxs: I'd hate to reign on your parade, but shouldn't a 4*4*4*4 be larger than this ? If a 4*4*4 has 4 little 4*4 gobans, then a 4*4*4*4 should have 16, no ? The above example has only 8... enough for a 2*4*4*4, but not 4*4*4*4.
cj: You are right in that it is a set of 2 3D gobans, (ie 8 boards) but they interact using 4D. Making 4 3D goban intersect (evenly) in the middle would probably require more than 4 dimensions, and certainly would not be representable in 2D (which was my aim in the first place). It would also require (as you point out) 16 4*4 boards, a lot more than I can fit on a 50cm*50cm floor tile. I guess its a 2*4*4*4 board.
jianying: One problem with 3D and 4D Go is the problem of knoted territories, that it is possible to construct two territories such that they are linked so neither can be said to surrounding anything. The whole idea of outside and inside becomes difficult to discuss.
For example:
It is hard to say whose teritory the square or the circle belong to
CJ: This is a problem in playing, as it can appear you have 'walled off' your territory, but there is still an approach that you missed... however even in normal go what constitutes your territory is still only 'that which the opponent won't play in' and neutral space is walled off at the end of the game anyway. The regions you describe are essentialy the neutral territory you get in regular go, and the 'problems' of seki still exist.
3D Tetrahedron Goban
Netrin: I've never tried to play this. In fact, I don't know how it could be physically constructed, but it is a 3D space where each point has four liberties. Visualise stacked tetrahedrons (triangle base pyramids). Stones are placed inside each tetrahedron rather than the intersection of lines. Notable features. An eye in the center requires four stones. On a centre side and edge (I think), three, but the corner requires only one stone.
![[ext]](images/extlink.gif) http://www.internetchemie.info/news/2008/aug08/images/neutrale-gold-nanopartikel.jpg
http://www.internetchemie.info/news/2008/aug08/images/neutrale-gold-nanopartikel.jpg
Another way to visualise, is rather than platonic solids, caltrop shaped lines, and stones would be placed at the center of each caltrap (with four lines of liberty).
![[ext]](images/extlink.gif) http://www.buckymesh.com/Design_files/res.jpg
http://www.buckymesh.com/Design_files/res.jpg
![[ext]](images/extlink.gif) http://www.grunch.net/synergetics/quadray/4spokes.gif
http://www.grunch.net/synergetics/quadray/4spokes.gif
Instead of a massive tetrahedron (composed of smaller tetrahedron), it is probably best to chop off the corners, leaving 8 faces (four triangular, four hexagontal).
belab?:Isn`t it the same as diamond lattice?
Changing Size Goban?
Has anyone thought about having the board change size during the game? For instance, the board starts at 9x9 and then every 21 moves (so it alternates sizes on who gets to play first on the new board) the board expands 1 square in every direction (11x11, 13x13...)? Could make life and death very complicated...
-David Foale
Go on a general graph K
In standard Go, we can express the standard 19x19 goban as a simple undirected graph with 361 nodes and 684 edges, where 289 of the nodes have four edges, 68 of the nodes have 3 edges, and 4 of the nodes have 2 edges. The nodes correspond to a position on the goban, while the number of edges indicate how many liberties a certain position has. Likewise, we can write the torodial 19x19 go board as a graph with 361 nodes and 722 edges, where all 361 nodes have four edges each. We can express the 4x4x4 goban in the three dimension variant above as a graph with 64 nodes and 144 edges, where 8 of the nodes have six edges, 20 nodes have five edges, 24 nodes have 4 edges, and 8 nodes have three edges. And etc, for nearly every other unusual goban listed in this article. The partially severed connection variant can also be expressed as a graph, but rather a directed graph instead of an undirected graph.
Considering this, what happens if we were to play on some general graph? We can imagine playing Go on, say a complete graph Kn, or a wheel graph, or the Herschel graph, or the Fano plane, etc, each with their own different connections and resulting different gameplay?
For instance, here is a K5 graph; one can draw this on a sheet of paper, for instance, and then place down stones on the nodes during a game of this go variant.

- Anonymous
73.168.5.183: Seems like Henry Segerman has already formulated something similar here: ![[ext]](images/extlink.gif) http://www.segerman.org/topologo/gengraphgo.html
http://www.segerman.org/topologo/gengraphgo.html
Symmetry superko on the complete graph
Patrick Traill: If you play on a highly symmetrical graph (such as a complete graph Kn), an aspect of superko is transformed from a highly unlikely obscurity to something essential: it seems plausible to forbid repetition of a position symmetrically equivalent to a previous position, as such positions are, after all, tactically indistinguishable so that a winning strategy in one works in the other. If we do this, assuming positional superko, the game reduces to a walk through the triangle { (x,y): x ∈ N ^ y ∈ N ^ x+y < N } where no point may be revisited (superko), a valid move steps in one’s “own direction” away from the origin (i.e. adds 1 to x or y, one’s “own component”) and, if the total becomes n resets the “opponents component” to 0 (if we assume capturing the opponent to be obligatory although suicide would otherwise be an alternative – otherwise one must set one of the components to zero); this must be relatively straightforward to analyse: combinatorial game theorists, do you know more?
Off Topic
The Goban is fine. Generalize to more players!
Go as it is currently defined is a zero sum game, without the possibility of cooperation. With more than two players and basically the same rules otherwise, it takes on a fundamentally different character. Here is an example implementation (in .NET 1.1 framework) ![[ext]](images/extlink.gif) Rob. There is only one rule, that if you are surrounded then you are captured. Capture is explicitly defined as 1) location in which to move has its liberty removed 2) stones with no liberties are removed from the board 3) the newly placed stone is put onto the board. The only difficulty I encountered in this definition is how to count captures in score: do you add captured stones to your own score, or do you count by subtracting your dead? ... this makes a difference when there are more than two players.
:I would say, by subtracting your own dead. If you add prisoners to your own score, you have two problems: If a captured group is surrounded by two different players, who gets credit? If you say, the person who played the capturing stone, then that allows a situation where one player puts their opponent in atari, and the other player makes the capturing move! You'd never want to put your opponent in atari, therefore, since it would be almost certain to allow your opponent to steal the points from you! Christina? (13 kyuu)
Rob. There is only one rule, that if you are surrounded then you are captured. Capture is explicitly defined as 1) location in which to move has its liberty removed 2) stones with no liberties are removed from the board 3) the newly placed stone is put onto the board. The only difficulty I encountered in this definition is how to count captures in score: do you add captured stones to your own score, or do you count by subtracting your dead? ... this makes a difference when there are more than two players.
:I would say, by subtracting your own dead. If you add prisoners to your own score, you have two problems: If a captured group is surrounded by two different players, who gets credit? If you say, the person who played the capturing stone, then that allows a situation where one player puts their opponent in atari, and the other player makes the capturing move! You'd never want to put your opponent in atari, therefore, since it would be almost certain to allow your opponent to steal the points from you! Christina? (13 kyuu)
See also:
NetGo
doraguma: try the NetGo rules on a standard board
Programs to play Variants or on Irregular Boards
- gobrett.jar: Wastl Sommer has developed
![[ext]](images/extlink.gif) this Java applet (running in the page) to display not only usual gobans (with four corners and four liberties), but more general gobans with any number of 'corners' and liberties, too. The applet (in the page) allows the placement of stones, but it is not really suitable to play entire games on large boards. No engine, no automatic removal of captured stones. All systems (Java applet). The source code is available.
this Java applet (running in the page) to display not only usual gobans (with four corners and four liberties), but more general gobans with any number of 'corners' and liberties, too. The applet (in the page) allows the placement of stones, but it is not really suitable to play entire games on large boards. No engine, no automatic removal of captured stones. All systems (Java applet). The source code is available.
- Bakaban written by
![[ext]](images/extlink.gif) David Bofinger allows to play on some variants of Go boards (torus, cylinder, moebius, sphere and some others). No engine! Read the
David Bofinger allows to play on some variants of Go boards (torus, cylinder, moebius, sphere and some others). No engine! Read the ![[ext]](images/extlink.gif) review on britgo.org and download the program there! For Windows
review on britgo.org and download the program there! For Windows
- Freed Go by Lewey Geselowitz: program to play all kinds of 3D and 2D boards. It lets you play on, among others, a sphere, cube, cylinder, and mobius curve. Ability to view the board in 3D. You can play against another person either on the same computer or via network (local or ...). No engine! It can be downloaded from
![[ext]](images/extlink.gif) Lewey's Freed Go page For Windows and Mac
Lewey's Freed Go page For Windows and Mac
-
![[ext]](images/extlink.gif) Jenn by Fritz Obermeyer creates a 3-dimensional grid. Jenn lets you play on all kinds of bizarre projective geometries. Windows binary and source code, no engine, automatic removal of captured stones.
Jenn by Fritz Obermeyer creates a 3-dimensional grid. Jenn lets you play on all kinds of bizarre projective geometries. Windows binary and source code, no engine, automatic removal of captured stones.
-
![[ext]](images/extlink.gif) 3D Battle Go was a program by
3D Battle Go was a program by ![[ext]](images/extlink.gif) Lukas Biewald, but there are no more download links at the moment (dec.2009). There were Windows binaries and source code for Linux. With engine! You can try to contact Lukas at doloreslabs.com (his company) or at linkedin.com;
Lukas Biewald, but there are no more download links at the moment (dec.2009). There were Windows binaries and source code for Linux. With engine! You can try to contact Lukas at doloreslabs.com (his company) or at linkedin.com; ![[ext]](images/extlink.gif) happypenguin.org has a picture of the program's appearance. Oh - it is not real Go: "instead of taking turns players shoot the stones into the rotating lattice". :-)
happypenguin.org has a picture of the program's appearance. Oh - it is not real Go: "instead of taking turns players shoot the stones into the rotating lattice". :-)
-
![[ext]](images/extlink.gif) Diamond Go by Geoffrey Dommett allows to play
Diamond Go by Geoffrey Dommett allows to play ![[ext]](images/extlink.gif) Henry Segerman's Diamond Go. Windows binary, no engine, no automatic removal of captured stones.
Henry Segerman's Diamond Go. Windows binary, no engine, no automatic removal of captured stones.
-
![[ext]](images/extlink.gif) 3Dimension GO by Ishihama Yoshiaki creates a Diamond Goban similar to
3Dimension GO by Ishihama Yoshiaki creates a Diamond Goban similar to ![[ext]](images/extlink.gif) Henry Segerman's Diamond Go, on the Mac (System 9?)
Henry Segerman's Diamond Go, on the Mac (System 9?)
- There are also some programs and PDFs to print out a Round Go (look there).
- Toroidal Go: A tool for reviewing games (copy/paste the SGF into the viewer) and for playing/editing:
![[ext]](images/extlink.gif) link to the online demo
link to the online demo ![[ext]](images/extlink.gif) link to the source code on github
link to the source code on github
![[Diagram]](diagrams/3/ba7ccc781843b57a4af575a323c0124e.png)
![[Diagram]](diagrams/0/6ce6aeb3363dcb1401e21b08ba45cd83.png)
![[Diagram]](diagrams/3/c696207b133bc55e8bfbfff26f8dad11.png)
![[Diagram]](diagrams/43/1153b265ce4b66b753742d6f7274d8c9.png)
![[Diagram]](diagrams/47/ba4a485e80cadc76b3d5e76d2fb12959.png)
![[Diagram]](diagrams/22/3638dda2eca2df00b3512ea7e18bf445.png)
![[Diagram]](diagrams/43/1545fc8c03eb20a5aa3f2749d84c8f56.png)
![[Diagram]](diagrams/14/b8e873d3413e4f860a4dd052a8675311.png)

![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)