Toroidal Go

Table of contents Description Strategy Wraparound: adding additional lines Examples of wraparound AI daoqi.org Online servers and tournaments Other links and resources daoqi.org Malcolm's blog Notes

Description

Toroidal Go (henceforth referred to as “t-Go”) is a Go variant which is played on a graph that can be seen as a normal board where the edges have been “removed” as follows: the edges “wrap around” horizontally and vertically; they link up with each other so all points have 4 neighbours; each point on the far left is linked to the point on the same horizontal line on the far right; similarly for linking up points at the top and the bottom.

In order to help players' reading, two techniques are used in computer software (t-Go clients and editors): “wraparound", described below, and panning (AKA “drag-and-drop"), described in toroidal go / maths.

The name Toroidal Go comes from the fact that this board fits naturally onto a toroid / doughnut three-dimensional surface. See toroidal go / maths for other mathematical considerations.

T-go is just one example of a family of go variants called edgeless Go.

Strategy

• In the fuseki on this sort of board, all groups are floating.

• In 11x11 toroidal Go, aiming to make eyes isn’t always easy, nor is it a good primary goal to aim at. One strategy can be to try to split the opponent into two eyeless groups and then aim at killing one of them. (from a blog post)

• Fuseki strategy for 11x11 4.5 komi t-Go (from an introduction to t-Go):

In the fuseki as Black I tend to aim for several things at once. I try to develop territorial frameworks (I choose this term instead of “moyo” because on an 11x11 board frameworks have to be fairly small). I try to make them large enough in scale so that White has to make thin shape in order to prevent them from becoming territory. I look out for opportunities to split White into separate groups with thin shape. I also try not to let my shape become too thin.

With White I attempt to limit Black’s territorial development without making overly thin shape; if neither player has large territories at the end there is more chance that the komi will swing the balance in White’s favour.

Wraparound: adding additional lines

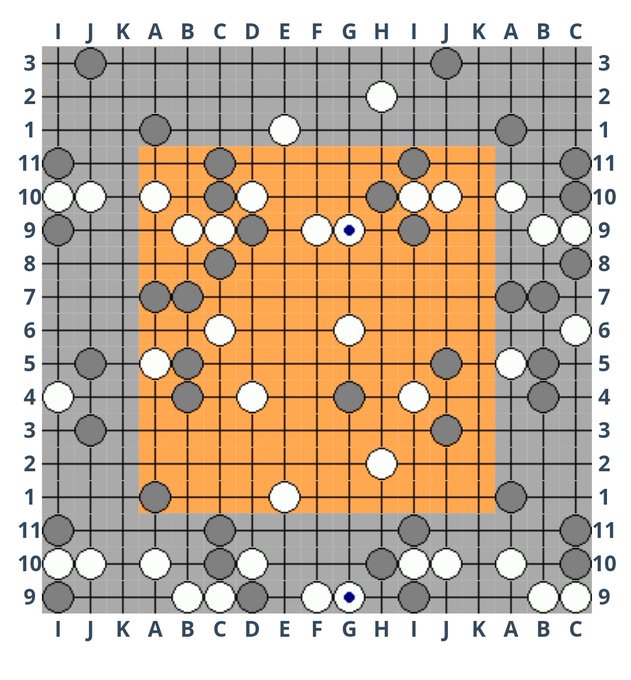
In n x n t-Go, when the board is represented as an n x n grid, a point on the edge of the grid is linked to the point on the opposite edge, which can be hard to visualise. There is a natural way of expanding the flat n x n grid by adding extra lines around it in order to make visualisation easier. Typically three or four lines are added; the number of lines added could be a matter of personal preference. The extra space added is called 'wraparound' in this article. Each point in the wraparound is just an additional representation of a point in the original grid, which we call the 'main area'. It’s not really necessary to explain more formally, when there are examples readily available (see the next section).

Ideally when wraparound is included, there will also be some way of easily seeing which part of the board is the wraparound area, and which part is the main area.

Examples of wraparound

• On LittleGolem, three extra lines are added to the 11x11 t-Go boards, and the background colour of the wraparound area is a different colour to the background of the main area.

Move #30 from a game on LittleGolem

Move #72 from a game on LittleGolem

• On a standard 19x19 board, 11x11 t-Go games can easily be played and reviewed by using the first four lines closest to the edges as wraparound; the main area of the board then consists of the 11x11 square whose corners are the four 5-5 points.

• A blog (also discussed below). In the games discussed on this blog, four lines of wraparound are added to 11x11 t-Go; signs are added to the points of wraparound that are adjacent to the main area (the “edge” of the wraparound) in order to distinguish between the wraparound and the main area.

A tsumego - White to play and win - from a blog post - after move #69

• The online viewer/editor for t-Go leaves the choice of the number of wraparound lines up to the person using the page; it also provides a choice of how to display the edge of the wraparound (no marks / box symbols / coordinates).

AI

daoqi.org

You can play online against an AI here: http://www.daoqi.org:8080/?lang=en-US.

The AI is based on katago and was made by Guoliang Cao. It is open-source; more details on github ( link). Cao made an announcement about this in July 2022 ( link).

You can play against an AI, or let AI play with itself. You can play even or handicap games, on small, medium or large boards.

The AI model was trained mainly on 19x19. So it's not as good on smaller boards.

To give you an idea how many handicaps you should use:

- on a 19x19 board, the strongest model can beat Guoliang Cao (an AGA 6D) with 6 stones.

- on an 11x11 board, Malcolm (French 1D) played two games with black. One loss (komi 4.5); one win (komi 0.5).

Online servers and tournaments

• On the turn-based game server littlegolem, all t-Go games so far have all been on 11x11 boards, with 4.5 komi. All games played on this server can be viewed inside it, and the SGF for the games can be downloaded too. Several tournaments have been played on it, as described below. It is also possible to play turn-based t-Go games without registering to a tournament. T-go tournaments so far:

1. As of July 2021, the ongoing “Infinite tournament” has 21 players registered. It is set up as a type of “ladder” tournament:

   “Max 1 challenge
   Max 2 defense
   Play with the same player after 14 days
   Challenge up to CEIL(SQRT(order))
   If challenger won game, overtake his opponent.”

2. There was a previous version of the “infinite tournament” which lasted almost 8 years. Link. The following statistics for this tournament were extracted in July 2021 by William Fraser:

   Players: 129
   Games(*): 1497
   Rounds: 138
   Start date: 2012-11-05
   End date: 2020-10-28
   Average length in moves(*): 76.35
   Average length in days(*): 65.67

   (*): excluding games with fewer than two moves.

3. One-off tournament on littleGolem with 7 participants; 14 games were played: link

• The Go Without Borders project http://www.gowithoutborders.com/ is an online server where players can meet to play 9x9, 13x13, or 19x19 games. Alternatively, users can download the free client application to play two-player games on their own Windows or Mac PCs. This server provides panning but not wraparound ^[1].

• Torigo server Torigo.io. Provides panning, but not wraparound. Mobile-friendly; for 9x9, 13x13 and 19x19 board sizes. As of September 2022, players tend to meet up on Thursday evenings from around 6pm (Paris time). There is a Discord channel too for this server: link.

• Variant go server implements t-Go for board sizes: 5x5, 7x7, 9x9 ... 19x19, 21x21, 23x23, 25x25. Wraparound and panning are both provided. Other variants can be combined with t-Go on this server, so it is possible for instance to play phantom t-Go. This server lets all games that have been played be viewed online.

Other links and resources

• “t-Go editor”: an online open-source tool for playing, editing and reviewing games (for existing games, you can copy/paste the SGF into the viewer): link. This tool provides panning and wraparound (with 0-7 lines of wraparound).
• T-go is called Daoqi / 道棋 by some Chinese people. There is a SL page about it: (link). On the Daoqi site there is an SGF editor (with an interface in Chinese) (based on Maxigos) that has been adapted for t-Go ( link). There are many articles about t-Go, mostly in Chinese ( link), and many SGF files of games, including over 1000 AI games ( link).
• The SGF editor q5go supports toroidal boards as of version 0.4. There are two lines of wraparound; panning is not provided. Boards can be cylindrical? and non-square: any m x n board is allowed, with m and n between 4 and 25 included. It can save and load t-Go games in a slightly non-standard format, and you can modify a normal SGF file: find “GM[1]” and replace it with “GMq5go-1?", and add a “TO[3]” property to the root.

daoqi.org

Mentioned above in the AI section, daoqi.org also can also serve as an online t-go board, letting two players play together (using the same device). It has panning and 3 lines of wraparound.

Malcolm's blog

• An introduction to toroidal Go: an article including three sample games (2017-06)
• a big fight in a t-Go game: blog post with two games and some analysis of the first game. (2017-10)
• a big fight in a t-Go game (2): deeper analysis of the first game in the previous entry. The comments are embedded in the game viewer; this was a “world premiere” (the first time ever such a commentary of a t-Go game was published online).(2017-12)
• A commented game: “some exciting moments and some interesting shapes” (2018-03)
• Divide and conquer (1): it lived too easily! (2018-05-01)
• A commented game with a shape problem (2020-05-01)
• A lucky escape and a tricky whole-board problem (game commentary) (2020-08-23)
• A big capturing race (Sighris vs Bernhard Herwig) (2021-07-04)
• Catching up in the endgame (2021-07-18)
• A successful invasion with a tricky endgame (2024-04-16)

The SGF with variations and comments for the items above was all written using the “t-Go editor” tool mentioned in the previous section.

Notes

[1] As far as I (Malcolm) know - I haven't checked this yet.