Edgeless Go

Table of contents Definition Locally Grid Edgeless Go Examples Locally Grid Go Edgeless Go but not Locally Grid Not Edgeless Go

Definition

A Go variant is a member of the Edgeless Go family of variants when:

1. The rules of play are the same as normal Go.
2. The board is finite, and every intersection has four neighbours - so there are no edges or corners.

The second condition just concerns the Unusual Goban upon which the game is played. So the term “edgeless Go” can also be used for Go boards without reference to the rules.

In mathematical terminology, the second condition just says the Go board being used is a finite 4-regular graph (see the wikipedia article on regular graphs).

Locally Grid Edgeless Go

Some variants which obey an additional condition are here called “locally grid” variants.

3. Every intersection also has 4 diagonal points where you can make a cross-cut - so, around every intersection it looks like a 3x3 grid ⊞.

A precise definition is given in the online mathematical article “locally grid graphs”. An interesting result in the paper is a classification of all graphs that are locally grid. It turns out that all locally grid graphs are embeddable in the torus or the Klein bottle!

Examples

Most of the following examples have been proposed by various people on various forums and social media.

Locally Grid Go

• Standard Toroidal Go (‘t-Go’) is an example of locally grid Go.
• Rectangular t-Go: as for t-Go, but on an m x n grid with m ≠ n, is an example of locally grid Go.
• Twisted t-Go: t-Go with a twist. This is another example of locally grid Go. The following illustration is taken from the article cited above ( “locally grid graphs”).

left: a (7,5) toroidal graph with a twist of 2. Right: an illustration of a “twisted torus” in 3-D space

• standard n x n graph embedded in the Klein surface

A Klein surface

Edgeless Go but not Locally Grid

• A tiny example to illustrate: you could play Go on the 6 corners of an octahedron. Each corner has 4 neighbours. But you can not cross-cut anywhere.

Octahedron

• Chamfered cube

The grid on the left is an Edgeless Go board

• Round Go

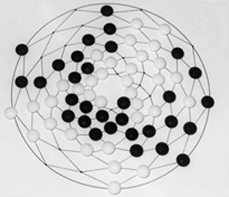
Round Go

Not Edgeless Go

• Cylindrical Go: in Toroidal Go all four edges are removed from normal Go; in Cylindrical Go only two are removed. This is not an example of Edgeless Go, as points at the ends (edges) of the cylinder have three liberties, not four.

• standard n x n graph embedded in the Projective plane

A projective plane

The standard n x n graph embedded in a projective plane provides an example of a graph that is not “edgeless Go”. This can be see in the following representation of the 3 x 3 projective graph - three lines of “wraparound” are added.

i h g c b a i h g
f e d f e d f e d
c b a i h g c b a
g h i a b c g h i
d e f d e f d e f
a b c g h i a b c
i h g c b a i h g
f e d f e d f e d
c b a i h g c b a

The point “a” only has three neighbours: “b”, “d” and “i” (twice!).

fool 2023-03-09: But with a different graph it should be possible to play Edgeless Go in the projective plane (but not Locally Grid Go, as proven in the linked paper)