Point popularity by move number

I (AshleyF) have recently been having some fun gathering patterns and statistics from a large collection of game records.

Statistics from games showing the popularity of points by move number. That is, "How popular is the 4-4 point on move 1?", "How popular is Tengen on move 20?". I did this for each unique point across every move. Below are sample results. This is a vastly simplified view.

Here is a GIF animation of it. Shaded in blue to indicate popularity. Points that are at least 80% as popular as the most popular point switch to red shading.

19x19

First 247 plays of 31,756 all pro games.

13x13

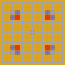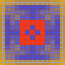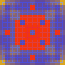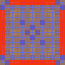
First 110 plays of 6269 amateur games. The same basic trend happens here as well only accelerated.

9x9

First 79 plays. 23,322 (!) games (202 of which are actually pro games). These games tend to be very short^[1]; by the 79th play the sample size has already dropped to 633.

It's difficult to represent with SL diagrams.

• - Most popular point.
• - At least 80% as popular.
• Circle - At least 40% as popular
• a - Played but less than 40% (towards the middle-game I stop labeling these)
• Points falling below 10% are not shown

Plays 1 - 4

Plays 1 - 4  

So, obviously the first four plays are in the corners and the 4-4 point is by far the most popular.

DamienSullivan: Might this be misleading? It seems surprising that komoku isn't 80% as popular as hoshi, did you account for symmetry? I note you did mention "isomorphic" way below, but it's still not clear.

AshleyF: Yeah, that does account for symmetry. Komoku is pretty close, but at least in my collection of games I show it at just over 69% as popular as hoshi. A quick double check in SmartGo against GoGoD shows very nearly the same result: of the 32,583 non-handicap games in GoGoD, 17,995 of them begin with hoshi compared to 13,364 with komoku. That's 74%, maybe slightly higher because GoGoD has a lot of older game records... Still not quite 80% though.

Play 5

Play 5  

You can see that play #5 is much different. Kakari, Shimari and long extensions have started.

Play 11

Play 11  

Through play #11, we continue to see the corners being settled and long extensions.

Play 29

Play 29  

By play #29 the a corner approach is still the most popular point. And the 3-3 point comes in second (90%). Higher approaches and extensions on the third line come in next (80%).

Play 39

Play 39  

By play #39 things have officially moved to the third and fourth lines along the sides. Strangely (to me anyway) the 3-3 point remains 90% as popular as just below the star point on the side ().

Play 66

Play 66  

By play #66, things move from the sides to the center.

Play 105

Play 105  

By play #105 it's truly all about the center.

Play 142

Play 142  

Around play #142 things begin to move back to the sides but on the second line now.

Play 199

Play 199  

By play #199 we can see that the corners are certainly settled as well as the third and fourth lines. Action is still going on in the center but common play has clearly started to move to the second and even first lines.

Play 210

Play 210  

Here the center action begins to die down and the first line becomes the most important.

Play 257

257  

This continues until the first line sides are literally all that's left. It's the same through the end of the game.

[1] It takes 247 moves on 361 (19x19) crossings before the number of games played drop below the significance level, 247/361. On a 9x9 this is 79/81. This is a bigger ratio, so in 9x9 it takes more moves to fight about the same size area than on a 19x19 board. In other words the 9x9 games are relatively longer. -- mAsterdam

Alex Weldon: This is fascinating, and the diagrams are beautiful. Perhaps our proverb "Corners, then sides, then center," should be adjusted to "Corners, then sides, then center, then sides again." :-)

Evpsych: Cool! Can you summarize your algorithm?

AshleyF: Very simple algorithm. Implementations differ, but conceptually create a three-dimensional integer array of 19x19x300 to track counts of plays at each point across 300 moves. Read through 32,000 pro game records (SGF files) and for each point played in a game, increment the point (and all isomorphic equivalents) in the array for that move number. That's it. Takes about 2 minutes to run.

Janne Jalkanen: This would make a wonderful 257 frame animation, methinks.

Charles Matthews: These are fascinating new sources of insight and questions.

mAsterdam: I would like to share in the general awe with an original compliment but I can't think of anything nearly as nice, brilliant or insightful as what you show us here. Remember Koyaanisqatsi?

Fhayashi: How different do you think it would be if you did the same treatment to all of Lee Changho's games vs. all of Takemiya Masaki's games?

Karl Knechtel: You found no tengen openings, or even plays near there within the first few moves, in over thirty thousand games? Wow.

AshleyF: The threshold to get into the above diagrams is 10% as popular as the most popular point for a given move number so tengen doesn't show up. In the animation though, you can see a couple of faint flashes of blue at tengen in the early opening.

Klaus: I am deeply impressed, staring at this page with a feeling of awe and undescribable insight. I wonder if there is any break in symmetry within the first ten moves. Sure the first move is most likely to be in the upper right corner? An interesting use for these diagrams might be to check where the "good areas" might be before choosing candidate moves. (Assuming that there is a correlation between likely points in pro games and likely good points in our games.) It might for example offer a hint, when it will be important to switch back to the sides, considering plays on the second (or even the first) lines. This might be very useful for computer Go as well.

FireclawDrake: The GIF animations on this page seem to be broken, which is a shame.

Bonobo: Animations are fine for me, as of 2013-05-28