BQM125
9x9 Mirror Go Problem
(Sebastian:) This problem is taken from the Mirror Go page.
Problem:
Black was one kyu below, so she had 0.5 gyaku komi. This way, when White achieves the same area, he still loses.
Questions:
- Did White after move #19 still have a chance to win the game?
- Can any statement be made, from when on it is too late to win a game against a mirror?
At this point, after  , I realized that Black was playing mirror go. Was this too late or could I still have saved the game?
, I realized that Black was playing mirror go. Was this too late or could I still have saved the game?
 =
= 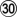
ferdi: assuming Black doesn't stop mirroring, the final position is still a win for white :)
unkx80: Note the reverse komi of 0.5. =)
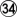 ,
, 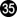 are mistakes. My answer below. [1]
are mistakes. My answer below. [1]
Bill: Hmmm. It appears that  was the losing move. If White omits the exchange,
was the losing move. If White omits the exchange,  -
-  , and then does not block at
, and then does not block at  , but continues to push at
, but continues to push at  instead, Black has to block at a, losing by 0.5 point, or allow mutual damage in similar fashion to unkx80s variation[2], which also loses because of White's eventual threat of atari at 5.
instead, Black has to block at a, losing by 0.5 point, or allow mutual damage in similar fashion to unkx80s variation[2], which also loses because of White's eventual threat of atari at 5.
ferdi: i wanted to point out that if white starts taking away liberties (say, at a, then b, c, and so on) he will win the "capturing race" if black mirrors the white moves.
(Sebastian:) Thanks, ferdi, this is an eye-opener. I was thinking they all had to be reasonable go moves. But why not risk sacrificing, say a, if this breaks the mirror! So, 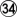 ,
, 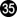 are mistakes because they make it too easy for black to stop that strategy due to the shortage of liberties in the SE corner? I don't see clearly how this would work out, though.
are mistakes because they make it too easy for black to stop that strategy due to the shortage of liberties in the SE corner? I don't see clearly how this would work out, though.
Andrew Grant: An anti-mirroring strategy is no use if Black has already won the game! If White tries playing 1 here, Black can answer locally, at 2, say. Since a failed invasion does not alter the score, Black will still be 0.5 points ahead. Of course, you can say that White's anti-mirroring strategy has "succeeded", in the sense that Black has had to stop mirroring, but Black still wins the game and White has no way of changing that. A true anti-mirroring strategy has two features: first, if Black continues mirroring he loses; and secondly, once Black is forced to stop mirroring White can then win. The above suggestion fails on the second count.
(Sebastian:) Thanks for the great explanation! So if we play under the assumption "black mirrors as long as it's not obviously stupid", is there any chance to save the game after move #19? Generally, it seems that the winning strategy is to surround a central group. But the shape was already quite rugged after move #19, so it may not have worked.
I'm just very disappointed that it's so easy for somebody to win a game with hardly even using one brain cell. This just isn't right. Or am I overlooking something?
Andrew Grant: I think you have to spot the mirror go before move 19 to have any chance of countering it here.
Of course, the real problem is the reverse komi. Since the only purpose that half a point komi serves is to prevent jigo, it could just as easily be 0.5 points komi to White, which would prevent all this nonsense.
Bill: I agree that you have to break the mirror early. (Wrong again! See unkx80's variation below.[3]) Just playing around, I came up with this:
Black starts with the tengen stone,  .
.
 prevents Black from easily securing territory with
prevents Black from easily securing territory with  . Maybe
. Maybe  should stop mirroring.
should stop mirroring.  is dubious.
is dubious.
BobMcGuigan: Andrew and Bill have advocated breaking the mirror early. As an idea in this direction, how about attaching on the tengen stone as soon as you see the mirror happening?
If you know your opponent is going to do a mirror strategy, say from past experience, try it right away:
It looks like white can win by forcing black into bad shape so white's moves make points but black's don't.
(Sebastian:) This is basically what Mellow did in the 9x9 Good Example after I warned him. So would you really play ugly moves each time you play that same person, just in case they might play mirror go again? If you do it only once, then they will just take a loss that time. But it would not keep them from trying it again with the next ususpecting victim.
BTW, this seems to illustrate an interesting point: Optimal play for mirror go is not optimal play if all replies are allowed. I suspect that this holds throughout the game. This may be not surprising, but it sheds light on a dilemma. Play between players of different strength does not work with optimal moves. If you assume optimal play, then of course black will win because komi and/or handicap is in her favour. Now mirror go pitches a player's strength against itself.
[1]
unkx80: The reason why I said that 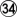 and
and 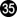 are mistakes has nothing to do with mirror go.
are mistakes has nothing to do with mirror go. 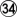 was play at a. Is this move neccessary, even when there is a black stone at b? No! By playing
was play at a. Is this move neccessary, even when there is a black stone at b? No! By playing 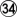 at a, White loses one point.
at a, White loses one point.
Same argument for 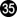 .
.
![[Diagram]](diagrams/37/3dc54443a5c6dc79305a4a78bae86490.png)
![[Diagram]](diagrams/23/24095da79d7e6799a7619aea4900b37f.png)
![[Diagram]](diagrams/27/0c8bfc80f1f730f66cf87f1db17a9c3e.png)
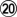
![[Diagram]](diagrams/27/e5ef000486b3ff3ffae331a8a157d793.png)
![[Diagram]](diagrams/14/f0abe2863d9493789a25cdddd4289c67.png)
![[Diagram]](diagrams/13/9d547d8e0bba8be9955021317e13ebfd.png)
![[Diagram]](diagrams/0/97d3b677b6b0726b69a30fe23e8cadf4.png)
![[Diagram]](diagrams/21/e696cd5af51d5a70aaeaec5e02662e35.png)
![[Diagram]](diagrams/4/419bdc9b113e3775e0df9d733b8991b0.png)
 is plainly a stupid mistake, and
is plainly a stupid mistake, and  looks bad, too. Even if Black
looks bad, too. Even if Black ![[Diagram]](diagrams/49/26996e79334881a728fed1985ad8c075.png)
![[Diagram]](diagrams/12/f7119d24db7139e570ba992b147d352f.png)
![[Diagram]](diagrams/51/9a1be4b672650428cce426c067a49bc0.png)
![[Diagram]](diagrams/22/e2df31e3768dd425dee20c0cff09d466.png)
![[Diagram]](diagrams/30/9e06b1877ab7457a7651f22a6a47ed8d.png)
![[Diagram]](diagrams/35/eb05304a5ccb6c9a9c15baf7d798d43d.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)