Optimal play
Optimal play is play that achieves the best results for the player, given subsequent optimal play by both players.
(Note: This is not a circular definition if play eventually ends, as it does in go, with rare exceptions.)
See also:
For a mathematical approach
For a philosophical approach
Discussion
Bill: Note to Willemien: While optimal play may be perfect in one sense, it is not the same. For example perfect play may also be play that yields the best chance of winning (but cannot be refuted, turning a win into a loss), even if the margin of the win is less than that by optimal play. The reason for using the term, 'optimal', is to distinguish it from other notions of perfect play. :)
Willemien: Thanks Bill, I know we are splitting hairs and YOU are the expert and I not even a deshi of you.
Can you give an example? (I like examples even if it is only an CGT tree )
Bill: No, I am not an expert. I am just reflecting my experience with the terminology. If perfect were not ambiguous, there would be no need for optimal. :)
Herman: Here's an attempt at an example:
![[Diagram]](diagrams/31/d387036bfcd084fc2e481d650a718786.png)
, a or b? (No komi).
![[Diagram]](diagrams/26/5b2b22e06549818cf902e0098e2dd50f.png)
is simple, and leads to a 1 point victory for black
![[Diagram]](diagrams/41/1bdf72e9ef8737f142e50472cca9d06b.png)
If black decides to hane, play might continue like this.
The first diagram might be considered perfect play for black. There are very few variations, and black wins.
The second diagram might be optimal play. Black is likely to win by more points than in the first diagram, because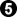 
was sente, so black got first play in both corners. (of course, white might ignore 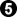to further complicate matters). Here, black is perhaps playing optimally, but is also taking a risk...
MrMormon: The idea of taking a risk directly contradicts the idea of optimal play.
anonymous #2: But we are talking about different meanings of "optimal" (or the difference between "perfect" and "optimal"). What if you are in a position where, with optimal play from your opponent, you will lose. Should you a) play a strategy that will minimize your point loss against an optimal opponent, or should you b) play a strategy that will lose more points against an optimal opponent, but will win against a greater variety of non-optimal opponents?
anonymous: on the page ![[ext]](images/extlink.gif)
http://senseis.xmp.net/?DoesKamiNoItteExist a proof was given that a winning strategy must exist for one of White or Black in no-komi go. It wasn't mentioned there that Black must have a winning strategy in no komi go. If White had a winning strategy then Black could pass on the first move and then follow the White winning strategy with colors reversed
![[Welcome to Sensei's Library!]](images/stone-hello.png "Sensei's Library")