Playing Infinitesimals
The play in infinitesimals is all about getting the last play. Chilling produces infinitesimals from go positions that have miai values of 1.
Both {0 |tiny-1} (the lower corridor) and ^ (Up, the upper corridor) have atomic weights of 1. Which should White choose to play in?
Should White play at a or b?
The difference game provides the answer. Let's have White play at a in this position and Black play at b in the negative position.
(Note on the diagrams. The stones that frame the positions are, by convention, alive.)
Each player has played the circled stone from an even position to set up the game. Does either player have an advantage?
The difference game favors Black, so White should play in {0|tiny-1} rather than ^. In fact, White should prefer to play in any corridor ending in a tiny before one ending in *.
That seems reasonable, because White's eventual threat is larger in {0|tiny-1}.
Both 0(2)tiny-1 (upper corridor) and 0(2)tiny-2 (lower corridor) have atomic weights of 2. Which should White choose to play in?
After  , White interposes
, White interposes 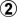 -
-  before
before 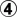 . White still gets the last play.
. White still gets the last play.
Since White gets the last play, regardless of who has sente, the difference game favors White. That means that White should play at a, the corridor with the smaller sente at the end.
Now that's a surprise, isn't it?
The key, it seems, is to save the hotter sente for later. Much like saving a big ko threat. :-)
This is not a case where the opponent's play is my play. Black prefers b, removing the larger threat.
Black can block White at a or b. Here a is sente, with an atomic weight of 0, b has an atomic weight of 1. Which does Black prefer?[1]
Here, too, Black plays sente and then gets the last play.
So Black should play a, taking away White's sente.
Note that the choice depends on the size of Black's threat versus the size of White's threat by playing at 4.
Also see
- Go Infinitesimals
- Corridor Infinitesimals
- Tinies and Minies
- Other Infinitesimals
- More Infinitesimals.
-- BillSpight
[1] Assuming Black is independently alive. --dnerra
I thought that was covered by assumptions of yose problems; but looking at that page, it could be made (more) explicit. -- Charles
Bill: I thought I covered that with the "note on the diagrams" above that said that the stones framing the diagrams were alive by convention.
![[Diagram]](diagrams/48/b2ad3030bb3eda4b22aa3c5a720cc755.png)
![[Diagram]](diagrams/17/97634d86a0376dc093da9648275a8818.png)
![[Diagram]](diagrams/39/aa470aa4828439d3266332bca241d31c.png)
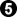 the rest is
the rest is ![[Diagram]](diagrams/32/a312e470ad2128427b1ba6eb46db55aa.png)
 ,
, 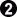 makes the rest miai. Black gets the last play when White plays first, too.
makes the rest miai. Black gets the last play when White plays first, too.
![[Diagram]](diagrams/15/d074368f16dd461195c97b8efd0e2911.png)
![[Diagram]](diagrams/22/3555b56ba89fd9efb74701b5e3b19064.png)
![[Diagram]](diagrams/10/474d4eaaf942310b2597af5dd6eccb6d.png)
![[Diagram]](diagrams/2/990b3131765ea21bfbaab798281b50cc.png)
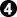 -
-  before
before 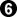 .
.
![[Diagram]](diagrams/20/3819ad8c7feadf1216cd596f3c783fb8.png)
![[Diagram]](diagrams/7/a921d28e49efcaf429ba980b0159c0ab.png)
![[Diagram]](diagrams/13/31841f6856eb55f6c30e0cadfe9e4d44.png)
![[Diagram]](diagrams/46/f12881056c4ba06b361cbf8218a4f0de.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)