Systematic Joseki / Why, Why not
I think that the wherether-it's-possible and wherether-it's-needed should be raised again because of the lack of "direct" sources and the lack of interest by sl content contributers... What do you think? (If you think it might be possible but.. please do suggest changes and ideas...) Reuven
For and Against the Project
- This might not be needed if all you want is a clicking in diagrams system - old pages could be adapted instead of remaking it all.
- Nobody actually uses joseki dictionaries
- It'd require a lot of work - Too much to cover a reasonable basis for it to work.
I don't think any of these are valid reasons, and generally I want to avoid all the negativity; "if it get's completed", "if it's worth it" "if someone bothers". Otherwise no-one will think the project will ever get anywhere and everyone will give up. I state now - this project will go ahead! Whoever helps and contributes, their effort won't be wasted because this project isn't going to die. Unless that is, anyone actually has a decent reason for why this project should definitely not go ahead? --Evan
nachtrabe: Addressing the points in turn: 0) Recreating from scratch gives a fresh start and lets you borrow what you need from the other pages, rather than being burdened by them. Both approaches are okay, but starting from scratch makes it less intimidating for people to contribute. 1) If "no one uses" Joseki dictionaries, why are they so popular and there are so many forms of them on the market and so many admonishments about memorizing joseki? It may be that they shouldn't use them, but they do. 2) Many hands and lots of time will make it a lot lighter in terms of the amount of work, and starting from scratch makes it clean and dynamic. Besides, the journey of a thousand miles begins with a single step.
Bob Myers: Hate to be pessimistic, but this entire attempt is stretching SL far beyond its capabilities. It could be very useful to have a wiki-like environment to cover josekis in depth, but josekis by their very nature are trees, and without specialized support in the SL wiki code these joseki pages are going to be unwieldy at best, unmanageable and unusable at worst. I'm not saying the idea is bad--far from it. I'd love to see support in SL for managing trees of variations. It's the same basic concept as what I suggested a year ago, namely to add built-in support for capturing terminology in various languages, in a way which allows that data to be specifically searched, organized, and processed (as in automatically creating glossary pages). The lame alternative that emerged to solve this problem was purely at the presentation level: to put the terms in different languages in a little box. An improvement, to be sure, but hardly the right way to handle multilingual terminology, something quite central to SL. I know the developers are busy and have their own priorities but unless they can provide built-in support for variation trees I think the whole Systematic Joseki projects, as well-intentioned as it is, is going to result in nothing more than a huge muddle. ++
Interesting - And what are trees, actually? What we'll have is a bunch of pages, where each page has it's place and is linked to what's above and under... Ohh yeah and the Systematic Joseki page as root... How do you think trees are implemented? (I did however ask in the meta discussion for some other features such as different color links in diagrams to separate joseki,trick and err moves - This kind of extra support would be nice even if not necessary as the categorisation is already there below the diagram...) Reuven
Gul: Might be stupid. I know the current Joseki thing isn't all that standard. But why don't you edit that? Isn't that the idea of Wiki? It would be wrong to have two separate joseki pages
Editing it wouldn't make it easier as we're talking here of a lot of page movement and separation - Using previous content is definitely a good idea though... Reuven
Evan: I don't see this as being the ultimate joseki guide possible, for that you need object orientated design and scripting. This is a wiki, the idea is easy collaboration and discussion, but at the same time I feel the need to add a bit more organisation and standardisation rather than the old joseki pages which were a little messy and inconsistant.
For those arguing to just edit the old pages, this would be just as hard to do as it would be to start afrest. The main idea of this new sytematic joseki is for each page to be a node, therefore the only way one would really edit the old pages to achieve this sytematic style, would be to create a whole load of new pages and transfer the old info across this is basically what we are doing, but at the same time we are taking the opportunity to create a whole new naming scheme, and making sure we do everything right. If I just suddenly started editing all the old pages to a new standard I think is good, but then after it's decided it would have been better to do it another way, then what? re-edit all the pages again?
So basically our aim to do a little bit of forward planning first before we start a frenzy of activity, I know this isn't the wiki style, but when you are creating hundred pages that are all meant to consistant with each other, planning is really essential. Then we start "converting" the old pages
I say "converting" but in reallity replacing the old joseki pages as we go along (before this project is finsihed) would be a bad idea for several reasons. Firstly, it would mean for months we will have a situation where half of the pages have a new style and half use the old messy unstandardised style. Secondly, it is actually harder to slowly work from within the old joseki guide than to creat a parallel project. Thirdly, it would mean we could't have a new pagetitle naming system, because it would have to fit in with the old one.
- This project will be in parallel to the old one in order to not interfere with the old pages, and to allow this one to develop without the pressure of knowing that the old scheme and content must always be preserved.
- This project is more complicated and very different to the old joseki pages, therefore the two are, in the practical sense, incompatible
- While extra presentational tools would be useful, they are by no means necessary for this project to suceed. The current tools easily suffice.
- I myself am happy to work on this project, I find it fun and hopefully I'll learn a little bit from it. While ignoring joseki may be a popular idea, trendy even, I still think a lot can be gained from studying and appreciating them. Maybe other people will be glad of an easier joseki guide too..?
Gul: Without doubt. I think if you are nearly finished (not possible I know:)) you should make the old joseki names aliases too these pages and ultimatly remove the old ones.
Rich: I agree with Bob; largely because it's not clear to me, since joseki dictionaries/encyclopaediae already exist, what is the advantage of making another on Sensei's? I would be suspicious of any joseki advice or exercises written by amateurs, and kyu-players in particular (as one myself). As a result, it seems that you're reduced to copying information from elsewhere, and run the risk of inaccurate information being added and potentially the burden of maintaining the pages.
It's certainly possible to do it on Sensei's, just curious as to what is gained by having it here (set against the man-hours necessary to have a halfway-complete tree for even one of the joseki like the taisha, nadare, magic sword, etc. Mind you, I've never really had a problem with the current (/old?) system.
Evan: Well it was obviously considered worthwhile the last time people started making joseki pages. A lot of the content on senseis can be found in more organised and professional form elsewhere. The point is, we want to create wiki versions, right? Maybe this project has little point for you, but as long as other people find it interesting, useful and perhaps even a little fun, then really I see no reason why the non-proponents should get it our way.
Evan: Plus, There is no reason why this project should take more man hours than the original one. In fact I am certain it can be done supprisingly quickly, with more accurate information and be pretty damn easy to maintain once completed.
Rich: Well, I don't see anyone getting in your way :) If you want to do it, you're welcome to. Just questioning the wisdom, is all.
The only reason I can see people complaining is if you delete the old page names; I think Aliasing is a good idea here, even vital, to save either storing the same information in two locations or forcing everyone to use your systematic naming system. I'd query the point that it will be "more accurate information", though - how do you intend to improve on what's beyond the grasp even of many high-dan amateurs?
Evan: Sorry got a bit overdefensive there :) I think if you look at what we have done already, we have included more different possible answers to each 'node' than what was previously on senseis, and that's just work in process. I think by having a more proffessional and orgnised look, people we'll be more likely to make sure the information is accurate, and add insightfull comments. That's the plan anyway. I am not saying we will be more accurate than proffessional joseki dictionarys though. Infact I'm not overly bother about the finished "product", I'm just as interested in what can be gained from the proccess of getting it completed.
Question our wisdom? I personally find this project very interesting, but really I don't think the wisdom of it is all that important. Even if it dies, which I think's unlikely, there certainly won't be any regrets on my part. "Just let the kids play".
Or maybe It's me that should just stop feeling the need to justify to everyone my reasons for doing things!
Shaydwyrm: What I'm hoping to see from this project is a treatment of some joseki at a much lower level than is available in the literature. For example, why in this joseki is the knight's move at 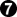 made rather than the one point jump at a, which appears safe at first glance? Things like this don't get attention in joseki dictionaries, maybe since they seem obvious, but these are details that an amateur discussion would easily reveal. We could never cover all of these points in such detail, but it would be nice to have a way of discussing them if questions arise.
made rather than the one point jump at a, which appears safe at first glance? Things like this don't get attention in joseki dictionaries, maybe since they seem obvious, but these are details that an amateur discussion would easily reveal. We could never cover all of these points in such detail, but it would be nice to have a way of discussing them if questions arise.
Exactly - Each variation would have a place, and a logical way of getting there. This is especially true for harder moves (than this particular one). And if we incorporate proffesional moves which aren't joseki, showing the context in which they're played... This isn't just "any joseki dictionary" - As mg said, they just aren't good enough - This is potentially our great way of analysing corner positions. In a relatively easy browsable way. We're also going to have browsing by results (Which joseki to chose when you want something) and a way of helping study of certain joseki localy/ as a part of a fuseki by adding related problems on relevant pages and maybe if the following comment is to be realised, even "sucking" all the problems from lower nodes would be possible and... Still think it's useless? I can go on... Well not really I'm too lazy for that... ;p (What do you think of template pages for joseki? I mean they're all mostly the same - And by actually spaerating them, we'd have a way to "dispaly all final positions" with descriptions and more... The joseki pages are as wiki as the rest, but they're different - They shouldn't have reffered by parent joseki pages and more unlike other pages... What if they were integrated with some different qualities for the specific purpose of corner sequence analysing? This could really benifit senseis, right? And maybe even generating an sgf sometime in the future? Or maybe sooner - Incorparating SGFs with variations by auto creating pages - Afterall the hardest part is the almost "automatic" one of creating links and such! See GuineaPigsFeedback.) Reuven
Malweth: What about Systematic Fuseki - Is this dictionary also on the way?? :) I would suggest a similar format to Systematic Joseki.
It could be done for common fuseki but I don't think it's going to happen as this project will have a lot of variations without having to worry about other corners. Once the joseki have sort by meaning(/result), people could use them to help with their fuseki. Reuven
Hmm... Guys... I've been thinking of it for a while now and my inability to understand what's the actual goal's depressing... It does seem like a joseki dictionary frame made for study - With extra excersices for nodes, the ability of discussing certain moves and/ or variations and adding/ changing them accordingly would benifit the Joseki Dictionary Frame and help people study the joseki, why does it go as it does and how to chose... But the buttom line is that it is a joseki dirctionary. Even if it's not the common, written and printed version but a wiki one which has it's merits (and disadvantages? Because a lot of discussion will be done by people whom you wouldn't normally find writting such dictionaries...) but as I said it a couple of times, it is a joseki dictionary however unusual a dictionary it may be!!! Reuven
Seems to me you have the goal spot on - to create a joseki dictionary in wiki format, with a focus on discussion of moves and interactivity. Due to being open to conversations, additions and comments by people of all strengths, it will be slightly more rough than professional dictionarys, yet the pages should still be neat and consistant, for it to be highly usable. Something along those lines anyway :) Indirectly we are therefore competing with other joseki dictionarys, just like the old joseki pages on this site were. Let us not pretend this is not the case. Evan
''Rich: This was one of my points earlier: it will not be slightly rougher, it will be orders of magnitude rougher. There are (AFAIK) no professionals contributing here or checking the data, and joseki are based purely on professional opinion. Pros regularly say that amateurs are poor at judging an even result - that's why we use joseki study. So, as a result, any information here (beyond basic move sequences) will either be copied from a professional somewhere else, or have a high chance of being wrong. Dictionary seems to imply some sort of reference work; I honestly believe that outside of a few basic, well-known joseki this won't be possible, as there isn't the go knowledge to do it. And gobase.org has a good introduction to simple, basic joseki already. As I said above, if you want to do it as an exercise for yourself, go ahead; as long as you are careful and honest about intellectual property there should be no problem.''
"slightly rough" was refering to the unprofessional feel and style, rather than the information being not so accurate. But again does this really if the joseki are not spot on and up to date to professional standards? I think not. No more really needs to be said; our reasons, justifications and capabilities have already been stated more than enough.
I am honest about intellectual property; I am honest to the fact that no one can reasonably claim copyright to the hundreds of joseki sequences that have long been out in the open, known and shared many tens of times already. -Evan
Rich: The sequences, no; however, reprinting variation diagrams and explanations from books or articles (for example), yes. People (including some on Sensei's) make a living from teaching and translating go material; if it just gets copied out and given away free, they won't do it any more. Not a personal dig at you, or restricted to the issue of joseki.
Evan: I would be kind of dissapointed if all we did was copy the wording from other people's work! But seriously, while I sympathise with people's needs to make thereselves a living, I stand by my belief that information, code, data, etc should ideally, be free and avaliable to everyone. Not that I'd go as far as purposely breaking copyright, but I will always support efforts where people are sharing information for free, even if it undercuts other's fee-required services.
Rich: If people can't make a living teaching go, the standard of go will deteriorate. At a certain level, the effort that goes into a subject needs compensation or it isn't worth it. I'm not sure, but perhaps you're unaware of the level of commitment it takes to become a pro? Why begrudge them the chance to make money, most of them are comparatively poor? Similarly, why discourage publishers from translating and publishing books on the subject? I just don't understand why that's desirable, or why people should feel motivated to devoting years of study and effort to discover and present new information to the world and not expect to be reimbursed.
Evan: "begrudge them the chance to make money". Sorry, but I'm all for people getting payed for work they do, please don't mistake me. But if someone who perhapes may not be as capable, also wants to do some work and offer their results for free, then that is also fine and in the world of the internet, ideal. Anyway I don't want to go too deep into this topic here. If you have problems understanding my viewpoint, then go and read up on GNU philosophy.
Rich: OK; all I would say is that I'm also familiar with and in favour of the GNU philosophy, but that is development from scratch. Joseki analysis comes from professionals; if one such professional decides to give his work away in line with GNU, great.
Surely most things under the gnu are written with known languages using known (well at least those which are unpatented) methods and so on... But it's not the point here. It'll take time to reach even the outdated joseki dictionaries we see these days. (Yes I feel rediculous when playing on a non western server where every 10k knows better than me) Not to mention reach a level at which it'd be a threat to such dictionaries. I'm one of the people who think that the work put into them is definitly copyrightable however joseki aren't: Did you ever notice how most joseki dictionaries have the same joseki in them and the same reasons for playing them? To be honest I don't have any dictionary but kogos. And you may notice in the future that I'll be adding (If I still have time...) variations which don't appear there. I am a kyu even if a low one but I've been taught about some principles and ideas and more important I studied current variations and others instead of just remmbering the order. They'll be my reasons. After I'll add them, will it stop proffesionals in the future from possibly adding them as explanations? It is a pointless conversation. It's doing what people were doing for a while on senseis only in a more ordered way, nothing less but plenty more, variations. The very argument here feels somewhat late or out of place.
Ohh and to all of you who don't believe that it can be done here,
there's a great thing written on the front page,
- Systematic joseki study is a great idea because it provides understanding.
- Using only tactics and coordinates as a system is a very bad idea because it misses the understanding due to strategy, evaluation and context.
- It would be very easy to fill the parent page with much useful contents if I were allowed to make extensive use of the various systematic approaches to joseki in my books. As long as Advertising On SL is unchanged, readers of my books and - for deeper systematics about tactics - some traditional dictionaries need to do so if they want to see on SL what exists in books. Whoever uses information should cite or state references properly.
- Why has SL not achieved the project yet? Because 1) it tried to be what it cannot be - an exhaustive tactical dictionary, 2) it did hardly at all attempt to expand systematic approach to strategy, evaluation and context. Not the aim of getting Systematic Joseki has been wrong but the previous ideas of realisation.
Tapir: You seriously miss the point here. Systematic Joseki was an attempt to make an exhaustive tactical dictionary by one move per page - not a systematic approach to whatever. Please, if you want to rant about advertising on sl or the failures of sl joseki pages, do this at a more suitable place. Systematic Joseki pages remain mainly for historical interest, so please don't edit for other purposes (unless you are committed to its in my opinion non-workable original idea and want to revive it). - You are free to write systematically using the reasoning of your books, but please take a little care at what pages you do and how this suits to the existing fabric of hypertext and of course it is always possible to make new pages too.
RobertJasiek: Is it possible that admins pay greater attention to page titles early? This would avoid missing a page's intention unintentionally. If a page was meant to be an exhaustive tactical dictionary, then it should have been called "Exhaustive Tactical Dictionary"! When, however, I read "Systematic Joseki", then I understand systematic joseki. - You say that I am free to write systematically using the reasoning of my books but currently I expect to be rewarded with deletion or meta-discussions if I invest a couple of hours. It seems more reasonable if first the joseki pages get a structure like the ko pages have gotten a structure. Then one can at least expect a page title to mean what it says. Afterwards adding contents will be easier. E.g., if I start reading at JosekiPages, I would expect SystematicJoseki to be the most appropriate page for systematic information about joseki. - What are referring to with "suits to the existing fabric of hypertext"?
Tapir: Yes, I know very well that every edit of yours is rewarded by an utterly useless metadiscussion. This would, however, be less of a problem if you would manage 1) not to write a detailed answer to every challenge and 2) take more care about the existing pages, whether your contribution fits in etc. and 3) would present your contributions with less of the "everything-else-is-rubbish" attitude which is so often at work. It is explicitly stated on the mainpage SystematicJoseki that this is an abandoned project, left here for historical purpose mainly. There are plenty of JosekiDiscussions on SL, where your edit would fit better. Please don't answer to this, but redirect your attention to a more suitable place.
RobertJasiek: A meta-discussion suggestion "please don't answer" does not work because everybody decides for himself whether he sees a good purpose with a continued discussion. - There is too much celebration of "this is an abandoned project"; why not simply delete it if it is that worthless? - If, e.g., page titles always meant what they write, if stated "facts" were always right, stated opinions were always reasonable and implied ideas (such as "only purely tactical dictionaries are worth comparing at all") were never dubious, then there would be less motivation to use what you perceive as "everything-else-is-rubbish" attitude.
Tapir: I did delete about 150 pages of this project last year, which sounds much but isn't if you present one move per page. The remaining pages are kept as a bad example to warn others before trying the same again.
Bass: Robert, have you taken a look at ![[ext]](images/extlink.gif) Josekipedia recently? It is a wiki like SL, but the entire site structure is based on josekis. It might not suit your purposes, but it's definitely worth a look.
Josekipedia recently? It is a wiki like SL, but the entire site structure is based on josekis. It might not suit your purposes, but it's definitely worth a look.
RobertJasiek: I see. Last time I looked, it was not interesting. I will have another look now.
![[Diagram]](diagrams/10/790c91fcd0ad444b6937096b6dedc4c4.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)