DougSGoBlog/Februari2004
Archived entries from Doug's go blog for February and March 2004.
30 Mar: Doing problems
I'm now in GGPB v.4. Much harder than v.3, a bit of a shock, but maybe I'm learning something.
A better judge of level might be problems missed during games. Here's one I blew: embarassing, but a step up from missing atari. To make it more interesting, identify every move that works for either side. Does the number of outside liberties ever matter?
25 Mar: Monte Carlo Go
More than a decade ago,
Bernd Br\"ugmann wrote what might eventually come to
be considered a classic paper: ![[ext]](images/extlink.gif) Monte Carlo Go -- assuming that his idea ever works out. It's based on a very simple idea -- play many random games to the end, and score moves based on how often they show up in games that you win. It's a kind of killer heuristic, or the enemy's key point is yours, but applied to the entire game. He claimed to get fairly good results (~25 kyu) for a program that knew nothing about go other than the rules. I was intrigued enough to even write and test my own implementation, although my results didn't seem to be quite as good as his. The concept has so far not been picked up by the community, perhaps because Gobble, Br\"ugmann's program, didn't win any competitions, or perhaps because there wasn't any obvious way to improve it by doing more work. A pattern database, you can tune or add more patterns, search you can tweak or search deeper. Still, new ideas are worth thinking about, particularly in an open field like computer go.
Monte Carlo Go -- assuming that his idea ever works out. It's based on a very simple idea -- play many random games to the end, and score moves based on how often they show up in games that you win. It's a kind of killer heuristic, or the enemy's key point is yours, but applied to the entire game. He claimed to get fairly good results (~25 kyu) for a program that knew nothing about go other than the rules. I was intrigued enough to even write and test my own implementation, although my results didn't seem to be quite as good as his. The concept has so far not been picked up by the community, perhaps because Gobble, Br\"ugmann's program, didn't win any competitions, or perhaps because there wasn't any obvious way to improve it by doing more work. A pattern database, you can tune or add more patterns, search you can tweak or search deeper. Still, new ideas are worth thinking about, particularly in an open field like computer go.
Recently, there has been some more work on the same idea. Piotr Kaminsky ![[ext]](images/extlink.gif) describes an implementation, and Bruno Bouzy has published
describes an implementation, and Bruno Bouzy has published ![[ext]](images/extlink.gif) two
two
![[ext]](images/extlink.gif) papers, reviewing the methods and describing how these ideas are being integrated into Indigo. It will be interesting to see what comes of this.
papers, reviewing the methods and describing how these ideas are being integrated into Indigo. It will be interesting to see what comes of this.
HolIgor: I have an implementation of this algorithm. I would not say it is 25k. It is still weaker than the crawler on everage. I did not know that the idea was discussed. I called this minimax algorithm in the case when at each move the program plays a lot of random games to find the best result with the stiffest competition. In a different algorithms the program kept a database of winning and losing moves but that worked much worse.
24 Mar: Another Holigor problem...
Black first is the 5k problem.  and
and  , in either order, both work I think. If White a, Black b. If
, in either order, both work I think. If White a, Black b. If 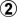 at 3, Black c. Did I miss anything?
at 3, Black c. Did I miss anything?
23 Mar: If it has a name, know it: Mochikomi
I'm not normally a fan of using Japanese terms, but I find it amusing that Japanese has a single word which means "an invasion which is a complete and utter failure, without any redeeming features or compensation anywhere on the board". In this fast net game, I was black. After I'd played  , probably a questionable invasion (any comment from a stronger player?), I was quite concerned with the possibility of it ending in complete and utter failure. White tried hard to kill everything, resulting in a capturing race with the UR white group. At my level, that's almost like flipping a coin, and indeed, White ended up one missed tesuji away from making the original invasion mochikomi.
, probably a questionable invasion (any comment from a stronger player?), I was quite concerned with the possibility of it ending in complete and utter failure. White tried hard to kill everything, resulting in a capturing race with the UR white group. At my level, that's almost like flipping a coin, and indeed, White ended up one missed tesuji away from making the original invasion mochikomi.
20 Mar: What will it take for computers to beat humans at go?
Strong humans, of course -- they can already beat weak humans, such as myself, at least occasionally.
In my opinion, three things, in order of increasing difficulty:
1. A decent evaluation function. There's a natural one: the current score, and I suspect it's pretty easy to compute given
2. A decent static estimate of stone safety. What stones can be captured, how threatened they are, etc., is crucial to everything. And finally,
3. A decent full-board search algorithm. This is the hard one. All the pattern matching and move generators are fine for ordering your search, but if your search algorithm is good enough, it's cheap to check the other possibilities too. It's hard not just that the search space is large, after all, that affects humans too. It's that the interesting parts of the search space are very deep (hundreds of moves) but sparse enough to be investigated by humans during play. I'd imagine that a functional algorithm might look something like Eric Baum's Baysian search, which spends as much effort on evaluating features which tell whether to search deeper as it does on position evaluation. It sounds nice, but by itself it must not be enough: Eric says his group spent two or three years working seriously on go (on a different idea), and gave up. I'd be interested to know what's wrong with this idea, but I don't want to spend three years of my life finding out.
19 Mar: Topological changes in capturing races
Topological changes are a familiar aspect of go, though they don't usually get called that -- cutting and connecting being the usual go-like terms. After the sequence of unkx80 from yesterday, White can do no better than atari and force Black to connect his two groups. This is a change in topology. Before this, we could call this a four group capturing race, linear,  -
-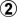 -
- -
-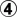 from left to right. But
from left to right. But 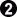 in the diagram connects the
in the diagram connects the  and
and  groups together, leaving
groups together, leaving 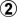 -
- -
-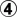 , a three group race with Black having the favorable position in the middle. And indeed, the
, a three group race with Black having the favorable position in the middle. And indeed, the 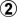 -
- race is seki, allowing Black to capture
race is seki, allowing Black to capture 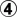 at leisure. This is termed a temporary seki.
at leisure. This is termed a temporary seki.
Note that the possibility of topology changes breaks the model for static analysis of capturing races. This can be recognized by the existence of a point like 2, which is a liberty shared by two of the black groups involved.
18 Mar: Examples of multigroup capturing races
Complex capturing races have been mentioned on r.g.g. again. One
example from real play is
![[ext]](images/extlink.gif) Shimada's position (BGJ 62:23 1984). This is a three-group capturing race
Shimada's position (BGJ 62:23 1984). This is a three-group capturing race  -
-  -
- 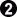 ,
,  eyeless,
eyeless,  has a one point eye,
has a one point eye, 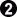 an almost filled four point big eye, no outside liberties, and a shared liberty on each side. If
an almost filled four point big eye, no outside liberties, and a shared liberty on each side. If 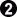 's eye was small this would be seki, but he can use the liberties from capturing the group to atari
's eye was small this would be seki, but he can use the liberties from capturing the group to atari  and win. The only hiccup is that there's also a ko to win, but since he can start the ko whenever he likes (including after the end of the game) it acts like bent-four-in-the-corner.
and win. The only hiccup is that there's also a ko to win, but since he can start the ko whenever he likes (including after the end of the game) it acts like bent-four-in-the-corner.
This example I found in the Fujisawa Tesuji Dictionary. The three black stones are in a capturing race with the white stones to the right, and are in serious trouble. The tesuji is to extend down with the dead stone to the left, expanding things into a four group capturing race. White must capture starting from the outside, and it takes long enough that Black has time to win the race on the right. This is an exchange, sure, but from the original position (down on liberties, 6-3, plus another stone in atari) it's surprising that Black got anything at all.
JoelR: 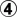 seems premature. What if White starts working on the outside immediately, and waits to see which way Black will play? The old line won't work, because White can play
seems premature. What if White starts working on the outside immediately, and waits to see which way Black will play? The old line won't work, because White can play  .
.
unkx80: Problem is, what happens when Black plays  ? There is a "seki" in the interior, but the exterior White stones are all dead, so Black captures everything.
? There is a "seki" in the interior, but the exterior White stones are all dead, so Black captures everything.
17 Mar: Fun with Japanese auctions
RussellKhan: I'm betting the owner doesn't play Go - maybe Go-moku or something, but even that seems a bit unlikely. Take a look inside the bowls - he's got a mix of black and white inside each. And the stones on the board don't seem to reflect anything in Go other than a 30kyu's game. The board setup could be Go-Moku, but that wouldn't explain the mix of stones in each bowl. What do you think?
DR: Perhaps they're just sloppy...
Very nice find, BTW. I wish I could buy it (I'd want this one over the other two you've got here).
![[ext]](images/extlink.gif) Another one -- what is it with turtles?
Another one -- what is it with turtles?
![[ext]](images/extlink.gif) A seven sun board for 2200 USD? If I guess right, that's something like 10c on the dollar, which seems ridiculously cheap even given a cultural bias against used goods. But I can't read enough Japanese to tell if it's met the reserve price, much less evaluate things like the wood, grain, and condition. Interesting anyway. Maybe I need
A seven sun board for 2200 USD? If I guess right, that's something like 10c on the dollar, which seems ridiculously cheap even given a cultural bias against used goods. But I can't read enough Japanese to tell if it's met the reserve price, much less evaluate things like the wood, grain, and condition. Interesting anyway. Maybe I need
![[ext]](images/extlink.gif) these books
to tell me what to look for.
these books
to tell me what to look for.
![[ext]](images/extlink.gif) 6 sun, 15000 USD -- but hey, it's signed by Otake. Finally, what I was looking for: memorabilia.
6 sun, 15000 USD -- but hey, it's signed by Otake. Finally, what I was looking for: memorabilia.
For those who don't live in Japan, ![[ext]](images/extlink.gif) Rinkya
says they make a business of being an intermediary, and also provide a nice interface. Here's a link
Rinkya
says they make a business of being an intermediary, and also provide a nice interface. Here's a link
![[ext]](images/extlink.gif) straight to their go stuff section.
straight to their go stuff section.
![[ext]](images/extlink.gif) Go fan
signed by Fujisawa Hideyuki. I want. But what do the words mean?
Go fan
signed by Fujisawa Hideyuki. I want. But what do the words mean?
Niklaus: 大道無門 (Daido mumen) litterally means something like "The great way has no gate" and (according to google) comes from the preface of the 無門關 (Mumonkan), a famous Zen text.
Most of the links above are broken or expired. Here is the link to all the ![[ext]](images/extlink.gif) GO stuff in Yahoo Japan Auction, provided by
GO stuff in Yahoo Japan Auction, provided by ![[ext]](images/extlink.gif) ok!shon Japan Auction.
ok!shon Japan Auction.
16 Mar: Capuring three
Shortly after deg pointed out the failure of my "capture three gives an eye" rule, I ran into the following problem (GGPB 3:196):
I find this problem interesting because it shows that I've learned something. The first time I went through the book, years ago, I sweated blood over the problems, and happily checked them off, as if I'd solved them once and for all. This one wasn't checked off, meaning that after much effort, I'd been unable to solve it. This time, it was pretty easy. Here went the train of thought:
"Black gets one eye from capturing the  stones, has half an eye
at a, and another one from capturing at b, for two clear eyes and life. That must be wrong, because we're supposed to kill him. The half eye at a is secure, so there must be some interaction at the edge, a way to defend against b and threaten the other eye at the same time. Connecting doesn't work, descent doesn't work, but...
stones, has half an eye
at a, and another one from capturing at b, for two clear eyes and life. That must be wrong, because we're supposed to kill him. The half eye at a is secure, so there must be some interaction at the edge, a way to defend against b and threaten the other eye at the same time. Connecting doesn't work, descent doesn't work, but...
this does, because the  recapture works with
recapture works with  to steal Black's last eye. Cool!" And yes, it's an example of a three stone sacrifice which doesn't give an eye, and one where adding
the third stone removes the eye.
to steal Black's last eye. Cool!" And yes, it's an example of a three stone sacrifice which doesn't give an eye, and one where adding
the third stone removes the eye.
12 Mar: The opening
I don't feel very comfortable with the opening, particularly on a big board. Sometimes I figure it doesn't matter, throw my stones around, and pretty soon find myself in the middle of a fight I can't win. I reread In the beginning, hoping it would help. The text seems simple but slippery, a quick read, but in one ear and out the other. I did wretchedly on the problems. I'd feel grateful if some of the moves I thought about appeared on the list of wrong answers. Sometimes it's obvious why I got them wrong (like when the answer depends on the details of when a particular invasion works, and the idea of invading never occurred to me, and my L&D isn't good enough to handle it even if it had) but usually it's just the wrong direction, no idea why. I tried some of the easy fuseki problems on goproblems.com, but didn't do any better. Maybe a book of opening problems would help.
As for closer fighting, I'm still in #3 of both GGPB and KPA. Slow going.
8 Mar: Algorithmic life and death
There are zillions of rules about life and death. Six live, eight die, seven is critical, except it's five in the corner; the list of big eye shapes, but watch for weaknesses; the tripod group is alive, but the door group is dead. Some get explicitly taught, others we just seem to pick up somehow -- eg. throwing in two stones leads to a false eye, but capturing three stones always gives at least one eye (doesn't it?).
deg writes:
unkx80: The capture three to make an eye rule has an (implied) assumption that the "corner" stone  must exist...
must exist...
Given the importance of life and death, you'd think there'd be some systematic study of it, but most of what I know of out there is training materials, some of it just problem collections, some with more organization, like the Davies book.
The computer go people have worked harder to systematize things. They have to, because learning through pattern recognition is much more difficult for computers. Examples of what that community has achieved include Benson's algorithm, which successfully identifies groups which are uncapturable under one-sided play, and the
![[ext]](images/extlink.gif) Chen and Chen
scheme of partially heuristic static analysis. Chen and Chen, the authors of HandTalk and Go Intellect, extend the usual big eye formulation through a series of rules which handle defects, not fully closed spaces, and internal prisoners. It looks simple enough that it's possibly even helpful to human players. Certainly I've spent lots of time evaluating all the possible ways of pushing and throwing in to something which is approximately alive, and still gotten the problem wrong. "Read it out" is the professional attitude, but it's helpful to know what the answer is first.
Chen and Chen
scheme of partially heuristic static analysis. Chen and Chen, the authors of HandTalk and Go Intellect, extend the usual big eye formulation through a series of rules which handle defects, not fully closed spaces, and internal prisoners. It looks simple enough that it's possibly even helpful to human players. Certainly I've spent lots of time evaluating all the possible ways of pushing and throwing in to something which is approximately alive, and still gotten the problem wrong. "Read it out" is the professional attitude, but it's helpful to know what the answer is first.
Played some more games, losses, mostly. But I did find a two stone edge squeeze outside of a problem book, which just about makes it all worth it.
Let's try to work out what Chen and Chen would do with this problem. It's based on a misremembered shape from James Davies, and I managed to get the answer wrong before checking with GoTools, so it's not completely trivial. In Chen and Chen's language, this is an imperfect pure eye region (not closed, but no internal prisoners). The controlled points, as best as I understand them, are marked with letters, f for a full eye point, p for partial eye point, based on the diagonal neighbors. Now we apply downgrading rule number 1, and reduce by one level for being adjacent to a false eye. The empty locations next to the eye region count (maybe?), so the p becomes false, its adjacent f becomes p, as does the upper right f.
There are contiguous full eye points remaining, so (if I understand correctly) we discard the partial eye points, and evaluate the region. It's a 5 point big eye, worth 1.5 eyes, so this group status is critical. And that's the right answer: White can live, Black can kill.
Unfortunately, I don't think I understand the algorithm. In particular, I don't see where the fact that  is there was used,
but it's necessary for Black to kill White. Or maybe it just gets the wrong answer in the case where
is there was used,
but it's necessary for Black to kill White. Or maybe it just gets the wrong answer in the case where  is a white stone -- after all, they describe it as heuristic.
is a white stone -- after all, they describe it as heuristic.
5 Mar: Playing go
I've actually been playing some go recently, as opposed to just writing about it. There's a tournament coming up, and (if I could make it, which I don't think I can) I'd like to play among the single digit kyus. So I'm training, doing some problems
(Graded Go Problems for Beginners 1 and 2, now working through 3 again, I never finished 4;
![[ext]](images/extlink.gif) Korean Problem Academy 1 and 2, now in 3; and
1001 Life and Death Problems again), playing a few fast games online. To improve, I need to make fewer mistakes. I suppose that's always true, but the disconnect between the kinds of problems I can solve as problems and the kinds of mistakes that decide my games is always astonishing. I missed an atari recently: not six moves deep, but an I-play, opponent-captures-large-group atari. Even playing fast, even if it doesn't happen every game, it's still probably the 30k mistakes that limit my strength.
Korean Problem Academy 1 and 2, now in 3; and
1001 Life and Death Problems again), playing a few fast games online. To improve, I need to make fewer mistakes. I suppose that's always true, but the disconnect between the kinds of problems I can solve as problems and the kinds of mistakes that decide my games is always astonishing. I missed an atari recently: not six moves deep, but an I-play, opponent-captures-large-group atari. Even playing fast, even if it doesn't happen every game, it's still probably the 30k mistakes that limit my strength.
I also played some 5x5 games against my kid. 5x5 is easier than 6x6, as he can count that high, but it does start to get into small board peculiarities. One ended up as a full board double ko seki -- that took some explaining. I refrained from introducing the concept of superko. With superko, even I have no idea what the outcome would have been.
Velobici Do you find that a steady diet of life and death makes your play tighter...less free...a larger number of more solid positions, while your opponent plays influence plays around the board? That seems to be happening to me at this stage (10kyu- 9kyu-8kyu nearly beat a 6kyu even ;)
DougRidgway On the big board, my usual tendency is to overextend, make too many weak groups, try and fail to kill something big and end up dying myself. I'm trying to play a little more solidly, settle groups, be a little more intentional about creating weak ones, but I don't think that's a consequence of the problems. I'm hoping that the problems will help me blunder less when liberties get short, and also in the endgame: is that really sente, etc. I play a fair bit of 9x9, which (as RobertJ puts it) is all endgame.
2 Mar: Even steven
Level 15 won 10, level 10 won 10. It looks like level 15 isn't better than level 10, or if it is, it's by not more than a stone. It could just as well be worse. That, or I screwed up when setting up the tournament, always a possibility.
And Kritz: yes, if both programs make a fundamental mistake, then deeper searching won't help. Based on this data, that's exactly what's happening.
kritz Is there an analysis anywhere comparing the strength of the program at levels 10 and lower?
Doug: I tried level 10 vs. level 1. Same result, except GnuGo really likes black. I must be doing something wrong.
geno: Have you tried playing GnuGo against some other go program? For example, gnugo at level 15 against Brand X 20 times, gnugo at level 10 against Brand X 20 times and so on? That would provide a constant-strength opponent for GnuGo, but one with presumably different tactical strengths and weaknesses. (I think gnugo is the strongest go AI, so you might need to track how many moku it wins by, rather than just wins.)
Doug: Nope, I haven't tried this, as I don't have access to others at the moment. And GnuGo, while good, is probably not (yet?) the best program.
1 Mar: Does GnuGo get stronger at levels above 10?
It gets slower, that's easily verified, but doing more work is no guarantee of better results. Some people on r.g.g. seem convinced that it makes no difference, but GnuGo developers aren't so sure. Certainly they bump the level up a bit for tournament play, but searching deeper does result in getting some problems wrong which it used to get right. The question is, is it stronger overall, and by how much?
It's too difficult to determine this by setting up games against people, so a little self-play series is in order. At komi 6.5, each side should win 50% if there is no strength improvement, and level 15 should win a little more if it is in fact stronger. If we want to use the chi-squared significance test, we need
xi^2 = ((W-0.5N)^2 + (L-0.5N)^2)/(0.5N)
to be larger than 3.84, the critical value for 1 dof at the 5% level (see any stats book), where W is the number of level 15 wins, L the number of losses, and N is the number of games played. That 5% is a type I error, how likely we are to find a difference by chance alone when they are in fact equal. How many games do we need to play to be sure of finding a difference at the 5% level? That depends on how much stronger level 15 is, and how willing we are to fail to identify a true difference (a type II error). Setting the type II failure to 10%, we'll identify a difference 90% of the time if we run
N = ((1.96*sqrt(p(1-p)) + 1.28*sqrt(0.5(1-0.5)))/(p-0.5)^2
games. p is the true probability of level 15 winning the even games, and how big a number we plug in determines how sharp the comparison is, and how long we have to run.
Let's suppose for a moment that we'd like to identify a strength difference of a full stone, and are willing to ignore lesser differences.
So what's the probability of the stronger player winning a game when there's a full stone difference in strength? This is also a crucial parameter for rating systems.
There are differing reports: ![[ext]](images/extlink.gif) AGA uses 0.83, Cieply reports
AGA uses 0.83, Cieply reports
![[ext]](images/extlink.gif) 0.70 for dan players in European tournaments, dropping to about 0.55 at the 10k level, the KGS
0.70 for dan players in European tournaments, dropping to about 0.55 at the 10k level, the KGS
![[ext]](images/extlink.gif) rating system
rating system
![[ext]](images/extlink.gif) uses 0.68.
Bigger differences make life easier: at p=0.83, we need 18 games,
at p=0.68, we need 75 games, and at p=0.55 we need 1,045 games!
uses 0.68.
Bigger differences make life easier: at p=0.83, we need 18 games,
at p=0.68, we need 75 games, and at p=0.55 we need 1,045 games!
I'm going to be optimistic, and run a 20 game tournament. So far, it's 2-2. We will see.
kritz I'd love to see your results. let us know if we can help. But is the analysis proper? if both programs make a basic fundemental mistake, neither will see it no matter how long it plays. This however may be meaningless for players like me who are weaker than GNUGO.
27 Feb: Broken symmetry?
In a symmetrical position, play on the point of symmetry, says the proverb. This problem (taken from
![[ext]](images/extlink.gif) Gobase KPA) sure looks like an example. Though symmetry
is a handy heuristic, it doesn't always work: all you can actually conclude is that if there is a unique answer, it's consistent with symmetry (eg on the line of symmetry), but there could be multiple answers, related by symmetry. In this problem, the sole symmetrical answer a doesn't work (answered by b or c). KPA gives the unique answer as b, and by symmetry, c should work as well. Does it? There is a corner not so far away, so it's not quite symmetrical. Is there any way for White to live after Black c?
Gobase KPA) sure looks like an example. Though symmetry
is a handy heuristic, it doesn't always work: all you can actually conclude is that if there is a unique answer, it's consistent with symmetry (eg on the line of symmetry), but there could be multiple answers, related by symmetry. In this problem, the sole symmetrical answer a doesn't work (answered by b or c). KPA gives the unique answer as b, and by symmetry, c should work as well. Does it? There is a corner not so far away, so it's not quite symmetrical. Is there any way for White to live after Black c?
23 Feb: Pass stones in the encore only
One way to handle life and death disputes in territory rules is to play it out in an encore, with pass stones used to ensure that needing to fill the liberties of the dead group in question
does not cost points. This variant is becoming increasingly popular:
![[ext]](images/extlink.gif) Ikeda Territory Rules I,
Lasker-Maas rules, Spight rules, and the
Ikeda Territory Rules I,
Lasker-Maas rules, Spight rules, and the
![[ext]](images/extlink.gif) rules for the
rules for the
![[ext]](images/extlink.gif) UK Go Challenge all use this
mechanism. In many (most?)
circumstances where area and Japanese rules
give different results,
this variant tends to adopt the area result. For example, you get to count one-sided points in seki, though you may have to falsely claim a life and death dispute first in order to get the encore started.
UK Go Challenge all use this
mechanism. In many (most?)
circumstances where area and Japanese rules
give different results,
this variant tends to adopt the area result. For example, you get to count one-sided points in seki, though you may have to falsely claim a life and death dispute first in order to get the encore started.
Another feature is that
you can refuse to connect a final ko (just like Go Seigen once did) and get an extra point, if you have enough ko threats.
Here's how to do it.
Don't connect the ko, instead play dame or pass if they're gone. Your opponent will eventually play dame for ko threats.
After dame are exhausted, each play on dame pairs using up a ko threat, the opponent passes, and you can pass too without connecting, stopping play. You connect in the encore, gaining a point. Essentially the same moves are correct under Chinese rules (though
![[ext]](images/extlink.gif) sometimes even pros get it wrong).
sometimes even pros get it wrong).
13 Feb: Happy birthday!
My daughter has taken to playing go when I'm not around. She'll get out the board and stones, find a go book, and study the book intensely while putting stones on the board. I wonder where she picked that up.
She turns two today.
10 Feb: Memorizing a pro game
In First Kyu, the protagonist gets stronger by simply sequestering himself with a collection of Go Seigen games. Just to see what this is like, I've decided to try memorizing a pro game or two.
I'm starting with the blood spitting game, one of the most famous in history, and (purely coincidentally of course) the only one which has a game record printed in First Kyu. Partly this is just to make the task easier: the strong story gives external significance to the moves (here is where the ghost played!), which should make them easier to remember. It seems to work: I know the first couple days of play pretty well, and it's been easier than I expected. But also, if I'm only going to end up knowing a few (or one!) games, they might as well be important ones.
6 Feb: Play moves you understand
"Play moves you understand" is a suggestion from Kageyama's Lessons in the Fundamentals of Go. There are various ways to read that of course: he uses it to mean not blindly copying fashionable moves from stronger players, but to do what makes sense to you. You're more likely to be able to follow up in a reasonable way, and (maybe more importantly) you'll have more fun.
Since I could recognize a fashionable move if it hit me in the face, I use it to mean, "Trust your reading". Self-confidence is important. Every false threat answered is an entire handicap stone. However, sometimes you're wrong. What then? Well, then you learn something. Accuracy in reading is important. It's better to get that lesson drilled than playing safe, disbelieving what you've read.
The opening scene in First Kyu is a tragedy in this form: a reading mistake, an unanswered threat, and resignation and death.
![[Diagram]](diagrams/36/f43e9af6599866e0162e619e61af3d61.png)
![[Diagram]](diagrams/37/8e83a5ad763f15c25f8e67140c9b12cc.png)
![[Diagram]](diagrams/45/ff6632991288c668036b3a2f180e05d7.png)
![[Diagram]](diagrams/0/46f7c910cc8a8839552a0ebac8bb140f.png)
![[Diagram]](diagrams/4/1ecfce23d6146ec0bc5c014801ba6037.png)
![[Diagram]](diagrams/15/cbc12836970054e486a365cdcc071458.png)
![[Diagram]](diagrams/12/9dbe15145cecdeca1c6e759e1cf4e0d8.png)
![[Diagram]](diagrams/9/3a1109ead992521467f41e2b60d74ed1.png)
![[Diagram]](diagrams/6/b960e48abb8ed6f2932b4b703f3fe61b.png)
![[Diagram]](diagrams/8/77a07790d1a77a5bf186cacad56eafaa.png)
![[Diagram]](diagrams/24/7e05d680ba856d8c08f54609a5d69700.png)
![[Diagram]](diagrams/0/e56c0e63c6dc3e7b57f29118ed05c285.png)
![[Diagram]](diagrams/50/0ba9e488561a5e5fbca1de50ae76fc78.png)
![[Diagram]](diagrams/10/ae53d6d170f88171b29fca6882fe4764.png)
![[Diagram]](diagrams/29/96e101908641c9e6fbdecf772273889b.png)
![[Diagram]](diagrams/30/df98aa544118e02bcec1a4188eff1a12.png)
![[Diagram]](diagrams/0/7525e70b22f81c0ecd104c6414622454.png)
![[Diagram]](diagrams/10/887609c179ac8ba54368386a27a74c00.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)