Doug's Go Blog/June 2003
June 2003 entries from Doug's Go Blog:
- Hikaru no Mo'
- One sided points
- The smallest living group
- Self organized criticality
- New rules
- Why do people argue about the rules?
- Neighbor topology is hard: NP hard
- 7x7 Go: the perfect game
- Higher order liberties
- More topology
27 June: Hikaru no Mo'
The ![[ext]](images/extlink.gif) Toriyamaworld scanslation of
Hikaru no Go has ended. HnG got me back
into go after an absence of a number of years, introduced me to
SL, and so on, and has been an important part of my go life.
Yes, technically it's good news, sure, because it means
it's been licensed, and will someday appear in English in an
authorized version, but still, I feel a sadness.
Toriyamaworld scanslation of
Hikaru no Go has ended. HnG got me back
into go after an absence of a number of years, introduced me to
SL, and so on, and has been an important part of my go life.
Yes, technically it's good news, sure, because it means
it's been licensed, and will someday appear in English in an
authorized version, but still, I feel a sadness.
This will be the last entry for a couple weeks, but I will return.
25 June: One sided points
A one-sided point refers to a point which may be taken by only one player, but does not actually yet belong to them. With best play, you go around collecting all your one-sided points last, while your opponent is forced to pass or make moves of zero value. These points seem to only happen in seki, and are strongly rules-dependent.
This is the most common example, also called one-sided dame. The groups are in seki, but they share 4 liberties. However, White cannot fill any of those liberties, because if she does, Black will be able to almost fill with a killing shape. Under area scoring, Black gets to pick up two more points here by filling liberties, but should not play here until after every dame is filled. Under Lasker-Maas rules, normally thought of as a territory ruleset, Black still gets these points, but shouldn't play here until the dispute resolution phase which uses area scoring.
The Black stones are alive in seki. The  stone is dead, but since surrounded points in seki are not territory, and under
J1989 Japanese rules only dead stones inside of territory can be
removed after the end of the game, Black must play to capture
stone is dead, but since surrounded points in seki are not territory, and under
J1989 Japanese rules only dead stones inside of territory can be
removed after the end of the game, Black must play to capture  before passing. He ought to do it at the very end, though, just
like the other one-sided point example. Some territory rulesets
give points for surrounded territory in seki: for these, Black loses a point by capturing. Be careful!
before passing. He ought to do it at the very end, though, just
like the other one-sided point example. Some territory rulesets
give points for surrounded territory in seki: for these, Black loses a point by capturing. Be careful!
One-sided points are excellent for testing your understanding of the rules and their consequences, and generating troublesome positions.
23 June: The smallest living group
Sure, the  stones are living in seki, but they are alive nevertheless. I find it impressive that two stones can live by themselves[1]. They don't even have a single real completed eye between them, though the Black group surrounding them does. It's a cute pattern, one that works only in the depths of the corner.
stones are living in seki, but they are alive nevertheless. I find it impressive that two stones can live by themselves[1]. They don't even have a single real completed eye between them, though the Black group surrounding them does. It's a cute pattern, one that works only in the depths of the corner.
On a small board, like 2x2, you can have a single stone living in seki, or (if you choose a 1x3 board) even with two real eyes. Those don't really count, because those situations don't happen on a real board. This one does, however.
If you believe in the virtual group concept, you might also say there are zero stone living groups, in places where an invasion could work. That's not really an actual group, though, just a potentiality. Once the stones in the invasion have been played and made life, there are more than two. Two stones is the smallest living group.
[1] You might argue that they are not living independently, since they require the external white stones surrounding the black group in order to prevent being captured. Well, yeah. Seki is different from having two eyes, sure.
Anonymous: Is OneStoneAliveInSeki the smallest possible?
That's a nice example. It requires another White group, also in seki, as part of the situation, so you might argue whether to count that group too, but still. Another example along those lines would be the single disattached stone in atari in the Hanezeki.
It's clear that seki is complicated. It reminds me of some table talk from a teaching game.
Dan player: Do you know about seki?
Me: Yeah.
Dan player: (places stone that reduces my meagre corner to zero) Now you know more.
Frs: Also known as: NoStoneAliveInSeki is the smallest possible. :-)
I got him back, though. I later surprised him by turning it into a ko, and losing the whole group. In retrospect, I might have misunderstood the reason he was surprised.
20 June: Self organized criticality
Not long ago, there was a
![[ext]](images/extlink.gif) discussion on r.g.g.
on the subject of connections between cellular automata and go. They look kind of the same, so why not? My suggestion was that it might be interesting to
look at scaling relations for random players and standard capturing.
discussion on r.g.g.
on the subject of connections between cellular automata and go. They look kind of the same, so why not? My suggestion was that it might be interesting to
look at scaling relations for random players and standard capturing.
It turns out, that's exactly what Mitsuhiro Itakura, a condensed matter theorist, ![[ext]](images/extlink.gif) has done. The results aren't particularly surprising: in 2D, you grow big clusters, as groups kill themselves off at all size scales. If you forbid suicide, then the size of clusters becomes limited: the size scale is around 20, which is (coincidentally?) about the size of the most commonly used board today.
has done. The results aren't particularly surprising: in 2D, you grow big clusters, as groups kill themselves off at all size scales. If you forbid suicide, then the size of clusters becomes limited: the size scale is around 20, which is (coincidentally?) about the size of the most commonly used board today.
So is it interesting, or is there "nothing there, don't waste your time" (as one participant of the rgg discussion said)? Well, hard to say. Amateurs and dilettantes are allowed to waste their time in whatever way they please, of course, but could it be worth taking seriously? For the physicist, it's hard to imagine random play and the go capturing rule corresponding to any process other than itself; whether physical, biological, economic, or sociological, so it's difficult to imagine that the results apply to anything. Without at least some cartoon of something being described, it's hard to call it physics. And for the go player, the properties of games played by random players say little about the carefully tuned games played by competitors. But still, I find myself interested. It's a waste of time, sure, but what isn't?
19 June: New rules
The very simplicity of the rules of go encourages experimentation. There are, of course, dozens of variants, games which are similar, or very different, but in any case distinct. But there are also many versions of the rules of go. We know that the way the game is played has changed over the centuries, and know something about those changes, but the process of those changes has been lost. More recent disputes and discussions are better documented, of which the Taiwanese rules committee chaired by Ing Chang-Ki was seminal, but the desire for change seems to remain.
There are two new rulesets I'd like to mention here. One is the ![[ext]](images/extlink.gif) Strasbourg rules. Commendably (and rarely), the philosophy behind the rules is clearly stated: it is to be a set of rules which complete novices can learn and play unattended. They have been translated into multiple languages, and have been the basis of a Flash intro to go. Straight evangelism, in other words. Scoring is stone scoring, which is equivalent to area scoring with a 2 point tax per group.
The ko rule is either just the simple ko rule, with long cycles undefined (the first introduction to the ko rule) or superko.
Stone scoring is not no-pass go, but isn't too far from it. I wonder if it wouldn't be possible to develop a variant of no-pass go that was equivalent to stone scoring; aimed at beginners. (E.g., a move is returning a prisoner or putting a stone on the board, suicide and passing is prohibited, first person who cannot move loses.) The idea would be to avoid counting entirely, and substitute filling in the territories during the game.
Strasbourg rules. Commendably (and rarely), the philosophy behind the rules is clearly stated: it is to be a set of rules which complete novices can learn and play unattended. They have been translated into multiple languages, and have been the basis of a Flash intro to go. Straight evangelism, in other words. Scoring is stone scoring, which is equivalent to area scoring with a 2 point tax per group.
The ko rule is either just the simple ko rule, with long cycles undefined (the first introduction to the ko rule) or superko.
Stone scoring is not no-pass go, but isn't too far from it. I wonder if it wouldn't be possible to develop a variant of no-pass go that was equivalent to stone scoring; aimed at beginners. (E.g., a move is returning a prisoner or putting a stone on the board, suicide and passing is prohibited, first person who cannot move loses.) The idea would be to avoid counting entirely, and substitute filling in the territories during the game.
The other is Yet Another Attempt at a Quote-Unquote Logical Japanese Rules, Robert Pauli's Logical Japanese Rules of Go. Fixing the Japanese rules is a game we all can play, and goodness knows, so many have: identify some "flaws" in the existing rules, contrive examples of those flaws, then propose a new set of rules which gives a different result for your examples but is not obviously equivalent to any existing set of rules. Then, try to convince the rest of the world, and in particular, the Nihon Ki-in, to adopt them. This last part is the toughie.
Me, I'm still working on understanding the differences in actual play between territory and area scoring. I know that they are "usually" within a point of each other, and (modulo seki differences) related by a chilling/warming relationship, which is "almost" invertible. So they are close. Well, we knew that; but how close? Berlekamp and Wolfe spent an entire book on getting the last point, don't tell me that now it doesn't matter. When do you have to play them differently? And, most important of all, which one is harder, and therefore morally superior?
Added: The diligent will note that I've
![[ext]](images/extlink.gif) asked this question before.
I must not have understood the answers the first time, because years later I'm still asking the same question. However,
Bill Spight posted the following problem in response:
asked this question before.
I must not have understood the answers the first time, because years later I'm still asking the same question. However,
Bill Spight posted the following problem in response:
Komi = 0.5, white to play and win, by each of area and territory scoring (counting eyes in seki). As you can see, it's really two problems. Black has one more stone on the board than White, so there are no prisoners, no handicap stones. There are no one-sided points in seki, no differences in surrounded points in seki, and ko-wise nothing more unusual than a garden-variety ten thousand year ko (I think that's what's in the upper left corner). Correct territory and area play ought to be just about the same, right?
16 June: Why do people argue about the rules?
The rules are an ever-fresh source of discussion and dissension in the go world. It's worth examining briefly why this might be so.
It's not like go is the only game where people talk about the rules. There was an important NFL game (American football) earlier this year which was decided by a referee's misunderstanding of some rule. (Not a judgement call about what happened, but failing to properly apply some rule -- i.e. a failure of law, not of fact; the kind of thing appellate courts exist to correct.) A few years ago a golf tournament was lost when the leader put a towel down on the wet grass to kneel on to keep his pants dry while lining up a shot. Golf has lots of rules, and it turns out that there is a specific rule against this: one unknown to the player, his caddy, as well as the tournament organizers and referees, but caught by a sharp-eyed television viewer who called in to have the error caught and the penalty assessed. There are also the endless controversies, both in principle and in practice, over the use of performance enhancing substances.
One of the principal difficulties is that these endeavors are pastimes, and fundamentally, any activity could occupy free time. The basis on which one might choose one activity over another, or refine the precise nature of one activity, are always subjective and rarely stated. I once read a commentary on doping by the head of an international center for sports ethics which, for philosophical justification for anti-doping rules, simply said that sport was "arbitrary". Why does baseball disallow corked bats, which offer no advantage, but allow androstendione, which does? No reason needed: it's arbitrary. At the highest level, it's difficult to do better than this, although in professional sports, business reasons are sometimes invoked. You want the game played to be interesting to watch on television, and you'll adjust the rules as needed to make sure that happens. You have to be careful, of course: go too far, and you end up with monster truck "racing" or professional "wrestling", activities best understood as some kind of dramatic performance or exhibition rather than as a competition. Still, the reasons not to do that can be understood inside of the framework of business considerations: competition is interesting.
For go, things are somewhat different. In the East, go connects with an ancient and honored tradition, and that tradition is part of the appeal of the game. A change which might act to loosen or even sever that connection would lessen the appeal of the game. No longer would you be treading the same path as those who have come before you. In the West, the game is less popular, and people come to it for a variety of reasons. An interest in things Eastern (languages, cultures, pastimes and people) is one; mathematical purity and simplicity is another. These different backgrounds generate different perspectives as to what the game is, and how and why it should be played. Disputes about what the rules should be reflect these underlying, and rarely stated, differences. No other competitive activity shows such a contrast of deep tradition and mathematical simplicity.
Another important factor is the smallness of the rules differences. You can play an entire game (indeed, many games) entirely oblivious to whether territory or area scoring is in use, whether suicide is allowed, what happens if a long cycle comes up, or even what the exact komi is. It's quite clearly all the same game. Try playing football without knowing whether you're supposed to pick up the ball and run across the field or kick it into a net. If the differences were larger, there would be a schism, and the playing world would divide into multiple related, but separate games. It is the very irrelevance of these rules differences which allows their continual debate.
Andrew Grant: Your football analogy is better than you probably realise. At the inaugural meeting of the English Football Association in 1863 there was a major argument over whether or not to allow handling the ball. At the time different clubs played by different rules and the FA was set up partly to bring some order out of the chaos. The anti-handling faction won, whereupon the pro-handlers left the meeting, resigned from the FA and set up the Rugby Football Union. One game (football) became two (soccer and rugby). End of argument.
Charles On the other hand, most card games that are traditional exist in many related variants - it could be considered normal not to have agreement in detail on rules.
Hu: One game became five: football (soccer), rugby, American football, Canadian football (variant of American football or vice versa), and Australian football (variant of rugby, I am told). Poker is perhaps the card game with the most variants.
TheDude?: Now you're getting silly. How about Arena Football, or Indoor Soccer? or Hackey Sack? or NFL Blitz 2000 for PS-One? Where do you draw the line between variant and an entirely different game? This seems to belong with the discussion on English where we can discuss ad nauseum the difference between a language and dialect ("A dialect is a language without a nation" - Chomsky?). Practically speaking American Football and Canadian Football are essentially the same and the same is true (I'm told) for Rugby and Australian Rugby.
Andrew Grant: And there are others - for instance Gaelic Football, played in Ireland, or Rugby League, popular in the North of England. BTW, Australian Rules Football (NOT "Australian Rugby") is at least as distinct a game as American Football.
Quicksilvre Are you referring to the Tuck Rule Game that the Patriots won over the Raiders to advance to the Super Bowl? That wasn't the misinterpretation of the rules, as far as I know. That was an obscure rule used at a critical time that made a ball that looked like a turnover, not. Not that I'm nitpicking or anything :)
10 June: Neighbor topology is hard: NP hard
coz the boys in the hood are always hard
you come talkin that trash, we'll pull ya card
knowin' nutin in life but to be legit
don't quote me boy coz i ain't said sh-
What groups are next to what other groups is central to understanding capturing races between them, and perhaps other areas of go theory as well. I missed some possibilities the first time I went through the topological possibilities for group adjacency on May 25, and added a couple more on June 3. In fact, there's at least one more missed possibility:
-
-
-
|

Could there be others as well? It'd be nice to construct these systematically, so that we could know we had them all. Here's a straightforward method: start with the set of configurations of size N, and consider the configurations which come from adding first a black group, then a white one. The possible new configurations connect the new group to every (nonempty) subset of opposite colored existing groups. Now, delete configurations equivalent to ones already in the list, delete configurations which cannot be realized on a go board, and iterate as desired. Done!
There's one minor problem. Checking for equivalency is probably pretty easy (graph theorists correct me if I'm wrong on this; if so, that makes another problem), but determining whether the configuration can be realized on a go board is not. We should be able to realize a configuration on a go board if and only if we can draw the graph on a 2D sheet of paper without crossing edges. (Seems obvious, but might require a proof.) Drawing a graph without crossing edges smells like chip layout, which is known to be NP complete. (Briefly, it's easy to verify that a given solution drawing doesn't have any edges which cross, but there's a lot of permutations to try to confirm that it's impossible.) I'd be willing to bet dollars to donuts neighbor topology is just as hard.
The first unrealizable configuration occurs at six groups: three black, three white, fully cross connected (i.e. every black group connected to every white one). Seems like a good reason to stick to five groups or less.
9 June: 7x7 Go: the perfect game
Played a game of 7x7 this morning, and lost. I hate losing, which is probably my greatest weakness as a player, because it inhibits me from playing. Anyway, I was black, giving 6.5 compensation. Small board go is highly asymmetric, much more so than go on a big board, because the value of going first is a much greater fraction of the total board area: if 6.5 is about fair on both 7x7 and 19x19, then on a 7x7 the compensation/first move tradeoff is more than 13% of the final partitioning of points on the board, as compared to less than 2% on a big board.
In fact, there's a ![[ext]](images/extlink.gif) claimed solution for 7x7 worked out manually
by a group of Japanese amateurs. The result is B+9 without compensation, so giving 6.5 should result in B+2.5 against perfect play. I lost by 2.5, so I gave away 5 points more than my opponent. My first wrong move was
claimed solution for 7x7 worked out manually
by a group of Japanese amateurs. The result is B+9 without compensation, so giving 6.5 should result in B+2.5 against perfect play. I lost by 2.5, so I gave away 5 points more than my opponent. My first wrong move was 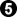 , which I played at
, which I played at 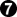 . By itself, that's only supposed to lose a couple of points, so there must have been other mistakes as well.
. By itself, that's only supposed to lose a couple of points, so there must have been other mistakes as well.
The rest of the perfect game is here. (The SGF I linked has Black capture at a, but this must be a typo: it's unnecessary, and loses a point under territory scoring.) According to the SGF,  could be at
could be at 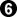 or
or 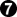 , but the rest is forced under territory scoring. Area scoring is a little more lenient for Black; there
are a few more optimal lines than under territory scoring, where Black surrounds less territory but can get the last move.
, but the rest is forced under territory scoring. Area scoring is a little more lenient for Black; there
are a few more optimal lines than under territory scoring, where Black surrounds less territory but can get the last move.
White has (in general) more options than Black, but the total number of variations is not so large that it couldn't be memorized. That would be an interesting project. Once completed, I could enter into 7x7 games; sure that I once knew the absolute best place to play, and if I could only remember it, I'd have a win in hand. My losses would then be due to failure of memory, rather than inherent weakness at go. I'm not sure if that would be an improvement.
4 June: Higher order liberties
There's a discussion about the concept of liberty happening in various places on SL (Secondary liberty / Discussion, MessagesToPeopleCurrentlyPresentInTheLibrary, Liberty). The two possible meanings for an extended concept are: number of moves to capture (including necessary approach moves as well as empty neighbors) and next-nearest (or further) neighbors, a la the higher order liberties I mentioned earlier. Terms like "virtual liberty" and "secondary liberty" get thrown around. No usage is particularly ingrained; "virtual liberty" has three hits on r.g.g, all meaning moves to capture; and "secondary liberty" is used once, meaning liberties gained by adding a stone, which is pretty well aligned with the higher order neighbor concept.
I first read of higher order liberties in
![[ext]](images/extlink.gif) ''Estimating the Possible Omission Number for Groups in Go by the Number of n-th Dame'', M Tajima and N Sanechika 1998.
Their context is computer go, but it's a nice concept generally. Charles Matthews' latest chapter of
''Estimating the Possible Omission Number for Groups in Go by the Number of n-th Dame'', M Tajima and N Sanechika 1998.
Their context is computer go, but it's a nice concept generally. Charles Matthews' latest chapter of ![[ext]](images/extlink.gif) Shape Up! also refers to this concept, talking about the nose tesuji as filling the liberty which reduces not only the number of liberties of the group (all liberties are equivalent for that) but also the number of liberties which can be gained by running away, ie secondary liberties. Many looser encircling moves can been seen similarly: a net fills not a liberty, but a second order liberty; approach moves against a corner restrict the movement of stones by cutting down the higher order liberties, and so on.
Shape Up! also refers to this concept, talking about the nose tesuji as filling the liberty which reduces not only the number of liberties of the group (all liberties are equivalent for that) but also the number of liberties which can be gained by running away, ie secondary liberties. Many looser encircling moves can been seen similarly: a net fills not a liberty, but a second order liberty; approach moves against a corner restrict the movement of stones by cutting down the higher order liberties, and so on.
3 June: More topology
I missed some of the possibilities in my discussion of capturing races; in particular, the number of groups on each side does not need to be anywhere close to balanced. So four groups could be three black, one white, and so on. To the possibilities below, we need to add two:
-
-
|

and
|
-
-
|

I think that's it for five or fewer groups.
One might also add the one group case:
It's trivial, but I'm fond of trivial cases, not least because they are easy to solve. In this case, the only possible outcome is that Black dies. Solved!
It seems to me that tiny introns shouldn't be considered active groups; they don't behave the same as a large group. In particular, capturing one doesn't assure life for an adjacent group. That might be good for part of the definition of an active group: it must be large enough that capturing it assures life for adjacent opponent groups. Otherwise, it's just a partial eyespace and a source of liberties. We can put a limit on the size of an intron: sans weaknesses, it's six, but (including weaknesses, a corner, etc) there are positions where up to 17 stones get captured but only produce one eye.
![[Diagram]](diagrams/29/8b05ad913414a09db7753c43d0cf61a4.png)
![[Diagram]](diagrams/45/3a5968d99a4bf0515455068ff1a1980d.png)
![[Diagram]](diagrams/36/a2a6633fb925844bbec8ec1d1afb5871.png)
![[Diagram]](diagrams/44/a67b3eeabe412a63510509d07c2b38ea.png)
![[Diagram]](diagrams/2/57d3b0c264669d4d278e5f74b97630c9.png)
![[Diagram]](diagrams/49/3c137d5bc57315fc745f7b58ccbb92df.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)