Butterfly
The butterfly[1] formation results from making not one, but two large knight's moves from the corner starpoint. It is generally considered to be inefficient, since as it stands the 3-3 point invasion succeeds, while its two wings don't radiate as much power as wider enclosures would.
This shape is referred to as Kannon-biraki in Japanese. Kannon is the Japanese name of the Buddhist goddess of mercy (Sanskrit Avalokiteshvara). In everyday speech, Kannon-biraki refers to a type of double (or "French") door, originally used in cabinets containing images of the goddess.
A duller name would be 37-44-73 enclosure. This is one of a number of unusual three-stone enclosures that are being seen more frequently in pro games.
3-3 point invasion
This sequence occurred in a game of Dosaku (in 1679 against Fukuo Genko, 3h - after Dosaku "a" black chose to not play ko and decided to kill white 7 with "d", Dosaku responded with "e", and then "f" followed) and also in a game Yu Bin-Seo Pong-su in 2000.  at a,
at a,  at b,
at b,  at c sets up a ko; if White wins the ko the damage to Black's position will be serious, so this may almost be a picnic ko from White's point of view.
at c sets up a ko; if White wins the ko the damage to Black's position will be serious, so this may almost be a picnic ko from White's point of view.
If White really wants to avoid ko, she could play  here, in place of c, for unconditional life.
here, in place of c, for unconditional life.  at
at  looks intimidating, but is an overplay.
looks intimidating, but is an overplay.
 is the answer.
is the answer.  is forced, whereupon
is forced, whereupon  threatens bent three life, requiring
threatens bent three life, requiring  . Now White unleashes
. Now White unleashes 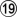 , forcing
, forcing 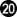 due to capture three to get an eye. After the cut of
due to capture three to get an eye. After the cut of 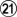 , Black is in pieces.
, Black is in pieces.
Query part I: Following the previous sequence but without playing the eye-steal - This is still a better reduction than the second diagram isn't it?
Query part II: Assuming the aji on the outside is just too much worse and the previous diagram ends up better, then I guess this is probably a fairly interesting continuation to have in the page (even if just for ko threats. As far as I can see, :w17: is required here for life, else it seems the vital point. If tenuki, then:
This kills?
IronChefSakai: You are missing a move here. If Black descends at 16, White can just connect at 20. After that White is alive since 18 and 19 are miai.
Other invasions
In practice, Black probably played at least one of the marked stones as a checking extension against a corresponding white stone. That makes the marked points interesting as possible invasions for White: if they connect out, a weak white group will gain in strength.
Alternatives
Black 1 here is the normal idea. The invasion point at a is then just some bad aji, not something White can use successfully at once.
b in place of  is solid play.
is solid play.
Query
spindizzy1976 This is a situation which I have been caught in recently, where I tried to invade in a 2-stone handicap game. At first glance it looks like playing at a might give a ko, but actually maybe not? Anyway, I connected at b and ended up dying. Can anyone suggest what I should have done? Is it impossible to invade here?
kb: Playing at a gives a ko. It is probably your best option here - especially if Black is strong on the outside (Black has at least the marked stone supporting the butterfly formation). You can try to run but most likely you will be cut and die. If you are strong in the surrounding area, go ahead and run - punish your opponent for their overplay at  .
.
Another variation
What if Black plays  as shown here? How do we live unconditionally?
as shown here? How do we live unconditionally?
[1] Apparently a non-standard term coined by Charles Matthews.
Not. The term has been around for decades.
![[Diagram]](diagrams/31/8ee5388ff950bce081b25c9c9a9545d7.png)
![[Diagram]](diagrams/32/8c5c2b0fa2444bfbef4dcfb50871f22a.png)
![[Diagram]](diagrams/31/f18851d7c28c1cd8a3ea89b90ee8e18f.png)
![[Diagram]](diagrams/22/0fc84b949ded54aa44b95b921da221c5.png)
![[Diagram]](diagrams/15/dec0422ef5dc6ebcb3a099d5b0ad5692.png)
![[Diagram]](diagrams/6/e190c9d454f1399c0be34e0e8e4ba9ac.png)
![[Diagram]](diagrams/25/a157d41cfeca084d582ca4d57281a2b7.png)
![[Diagram]](diagrams/44/2cc012ab655d1d67b96626bc40143653.png)
![[Diagram]](diagrams/0/0629cb2f1e8230429b41cebf8d8d8eeb.png)
![[Diagram]](diagrams/40/0f963fcb9153f3df2104375c2f609c7b.png)
![[Diagram]](diagrams/3/1dd98d7ca56fd7303fb7d56aa8920a75.png)
![[Diagram]](diagrams/42/39b9aac8b80fcdf3d4fa756d9305419c.png)
![[Diagram]](diagrams/49/33fc444748e1eda7f9bf8b09da86dca6.png)
![[Diagram]](diagrams/13/b7a9b0eff2e85c8c5f0d9eb9807ddc68.png)
![[Diagram]](diagrams/27/bf454613e228dfe370850d7af6360d89.png)
![[Diagram]](diagrams/51/19715e633f21ebe188e3083b652073ae.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)