Basic endgame theory

In the endgame the life and death status of large groups has been settled, and the board can be divided up into a number of independent or nearly independent regions. The focus of the game shifts mostly to the borders of territory.

Per Tomoko Ogawa, By the endgame the board has been more or less divided up into separate territories, and most of the fighting tends to affect only two of them, occurring at a mutual boundary. The opening and middle game are much like a single large battle between two armies; the endgame is like a number of smaller battles going on in different places simultaneously.

That doesn't mean that attack and defense are not important anymore, but rather that they are used more for immediate gain than for long term strategic goals. The life and death of smaller groups may be unsettled, particularly if they depend upon ko.

In this article we first give a short introduction to basic endgame strategy, focusing mainly on the importance of sente and gote. We will then go into more detail on precise evaluation of endgame moves, introducing a new concept of sente and gote in the context of the endgame and their effect on the value of moves. We will explain swing values, count, local tally and average gain values, and their application in evaluating endgame moves.

After reading this page you should have a pretty good grasp of the value of any single move, which makes choosing a good one quite a bit easier. If endgame theory does not simplify things for you, one can fall back to basic reading with the aim of optimising the score and imagined scoring at the end of every move sequence.

Table of contents Principles Struggle for Initiative Mutual damage What is Sente? Sente in the endgame Other principles Swing counting Examples Is the Swing Value Sufficient? Sente and Gote Play sente first Average gain (miai counting) Value of a position (the count) The miai value of moves What this means for the order of moves Evaluating branches See also

Principles

Beginners often struggle with the endgame, especially against stronger players. They feel like they are being pushed around, points they thought secure vaporize before their eyes, and what they thought was a comfortable lead turns out to be a hopelessly lost position.

Struggle for Initiative

Initiative (or sente) is one of the most important concepts in go. Gaining and keeping it is as important in the endgame as it is elsewhere. To keep the initiative you have to play moves with a follow-up, that is open-ended moves. To gain it you have to ignore those of your opponent's moves which lack such a follow-up.

Beginners are often frightened about their territory and tend to follow their opponent around, because they overestimate the loss of not responding to moves that are seemingly sente. They can improve their endgame tremendously by simply considering alternatives to responding to every move the opponent makes.

Instead of letting yourself be pushed around, you can push back.

One prime example of this principle is the concept of mutual damage.

Mutual damage

Initial position

Pushed around

Mutual damage

Mutual respect

Here's a simple example of the concept of mutual damage. In the initial position, on a 7x7 board, both players have claimed part of the board. Black can now choose an endgame move.

The second diagram shows the typical way in which beginners get pushed around. threatens white's corner. White instinctively defends the corner with and , then the same process repeats at the top.

But White can do better. Instead of defending against , White launches a counterattack with . Now, Black has a choice. He can continue with his attack in the lower right, scooping out White's corner. But if he does that, White will counter by scooping out Black's upper left corner. Both players receive damage, hence the term mutual damage. In diagram three we can see that Black would actually take a larger loss than white. Black's corner is bigger and thus more vulnerable.

Instead of the third diagram, Black should settle for the fourth diagram, respecting White's counter-attack. In this diagram, both players have received small damage symmetrically, and the exchange is fair.

Defending where necessary is as important as not defending where unnecessary.^[1]

What is Sente?

The first approach is to simply consider the local sequence of moves you expect, and then if your opponent needs to make the last move we call it sente, other wise we call it gote. Although correct in theory, it depends upon whether your opponent will indeed play the sequence you've envisioned. This depends on the value of plays elsewhere. See Value Of Sente.

Let's look at an example:

White sente?  

Here's a sequence that seems to be sente for white. White plays first, black plays last, so sente for white.

But what happens if Black, the opponent, deviates from our planned line?

Black plays elsewhere  

Here's a possible point where Black can deviate. Black decides to play elsewhere with instead of taking gote to defend the cut at a.

White cuts ( @ )  

White cuts and devastates black's territory, the end result is quite drastically different from the earlier line we showed.

What's the loss?  

Compared to the original diagram, all the marked points are gone for black, and White captures 1 black stone.

The above devastation of Black's territory is painful, but Black got one move elsewhere (move ). If the gain made by that move was large enough, then Black may well have been right in playing elsewhere with .

From the above, we can learn an important basic principle:

sente depends on the size of the follow-up.

Often, the size of the follow-up is unclear. The above example is relatively straightforward, but what if we remove one stone, like this:

Black stone at removed  

With that stone gone, the size of the follow-up becomes a lot harder to calculate. After in the earlier follow-up diagram, the position was settled. In this position, white would be able to push up further.

This is a genuinely hard question, to which there is no easy answer. Even the most experienced players will, at some point, have to make an informed guess about whether a given follow-up is big enough to make a move sente. Here, experience is key.

[edit]

Sente in the endgame

Reasonable play  

If we take another look at this diagram, we can identify that was sente. The follow-up, shown earlier in the mutual damage diagram, is large enough that black must respond.

But there is another concept of sente and gote in the endgame, which is important in evaluating moves.

A move or sequence in the endgame is said to be sente if its follow-up is larger than the value of not preventing it. If you play such a move when the follow-up is bigger than the other moves on the board, then your opponent will want to respond immediately, and you will be able to keep sente, which means that you get to be the first to play elsewhere too.

We will ignore complex issues like ko for now. The above is sufficient to allow us to start tackling the question of what the value of endgame moves is, which we will examine next.

[edit]

Other principles

Other principles about avoiding losing points, neutral intersections, premature endgame; taking more than the opponent; best global and local choices; reading; other topics avoid more than half of the practically ocurring endgame mistakes and can be found in the literature.

[edit]

Swing counting

There are several ways to estimate the value of a move. We will first explain the basic principle of swing counting before we move onto more advanced concepts, such as the effect of sente and gote on the value of moves.

Swing counting, also known as deiri counting, estimates the value of an area of play by considering the swing, which is the difference between White playing first and Black playing first.

[edit]

Examples

Lets have a look at some simple example endgames positions, and see what their swing values are.

First Example

Initial position

Black plays first

White plays first

From the given initial position, we consider the resulting position after either Black or White plays first. The difference between these positions is:

• If Black plays first, Black gets the marked point, White does not get the marked point
• If White plays first, Black does not get the marked point, White gets the marked point

So the difference between Black playing first and white playing first is 2 points. This is what we call the swing value.

Second Example

Initial position

Black plays first

White plays first

Again we consider the resulting position after either Black or White plays first. The difference between these positions is:

• If Black plays first, Black gets the marked points, White does not get the marked point
• If White plays first, Black does not get the marked points, White gets the marked point

So the difference between Black playing first and White playing first, the swing value, is 3 points.

Third Example

Initial position

Black plays first

White plays first

Again we consider the resulting position after either Black or White plays first. The difference between these positions is:

• If Black plays first, Black gets the marked point, White does not get the marked point and stone
• If White plays first, Black does not get the marked points, White gets the marked point and stone

So the difference between Black playing first and White playing first, the swing value, is 4 points.

This method of putting a value on moves is reasonably straightforward.

Exercise: In the earlier section on sente we gave an example of not defending a cut. Revisit that example and try to work out the swing value between Black defending and White cutting and devastating Black's territory. Answer

Is the Swing Value Sufficient?

There are a couple of problems with swing values. First, a naive approach would be to simply calculate the swing value of every move on the board and then play the biggest one. This approach fails because it fails to take into account the very important aspect of sente and gote that we introduced earlier. Second, as we shall see, swing values do not always add up correctly.

Suppose we take the naive approach with the above three examples. Suppose all three are on the board in different corners, and there is no other endgame.

White plays first in the 4 point position

Then Black plays first in the 3 point position

Then White plays first in the 2 point position

White plays first and takes the 4 point move with --, then Black takes the 3 point move with 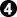--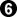, then White takes the 2 point move with --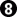. Using these values we might expect that White got 6 of the points in play, while Black got 3, for a net result of 3 points for White. But when we count the marked points White has 3 + 1 = 4 points, and Black has 2 points, for a net of only 2 points to White instead of 3. The naive method gives us the wrong result.

But that is not what swing values measure. They measure the difference between the results of a Black play and a White play. To make that comparison, what do we get if Black plays first?

Black plays first in the 4 point position

Then White plays first in the 3 point position

Then White plays first in the 2 point position

With this sequence White nets 2 - 1 = 1 point. That is 1 point less than White nets with the other sequence, and that accords with the swing values, since 4 - 3 = 1. White gets to play first in the 2 point position in either case.

But what we would really like to compare are different plays or sequences of play by White. Suppose that White takes the 3 point sente first.

White plays the 3 point sente

Then White plays the 4 point gote

The Black plays the 2 point gote

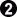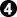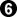White takes the 3 point move with ---, then White takes the 4 point move with --, then Black takes the 2 point move with --. Using swing values we might expect that white got 7 of the points in play, while Black got 2, for a net result of 5 points to white. So in this sequence, despite choosing a smaller move first, white made 2 points more.

However, when we count the actual points, we find that White gets a net result of 3 points, only 1 point more than the net result for White in the other sequence. The swing values do not tell us the actual point difference.

To compare the results of different plays or sequences when the same player plays first, use miai values, which tell how much each play gains, on average, as explained below. The miai value of the sente is the same as the swing value, but the miai values for the gote are half their swing values, 2 points and 1 point, respectively. With miai values in the first sequence White gains 2 points plus 1 point for the gote, for 3 points, while Black gains 3 points for the reverse sente. The net gain for White is 0. In the second sequence White gains 0 for the sente (see Sente gains nothing) and then 2 points for the larger gote, while Black gains 1 point for the smaller gote. The net gain for White is 1 point, which is 1 point more than in the first sequence. That is the difference in the resulting scores, as well.

Sente and Gote

Lets look at sente and gote in a little more detail. With the above three examples, we can say that:

• Example 1 is gote for White, and gote for Black
• Example 2 is sente for White, and gote for Black
• Example 3 is gote for White, and gote for Black

Instead of using the specific colors, it is more interesting to look at it from the point of view of one of the players. After all, you are playing only one of those colors. In general, we can differentiate four types of endgame moves:

Double sente

Moves that are sente for us, and sente for the opponent

Sente

Moves that are sente for us, and gote for the opponent

Reverse sente

Moves that are gote for us, and sente for the opponent

Gote

Moves that are gote for us, and gote for the opponent

Play sente first

A fairly effective approach, is to play moves in the order given below:

1. If there are endgame moves that are sente for you, play those. Those with the largest follow-up first.
2. Otherwise, all moves are gote for you so play the largest swing value first.

This approach is a lot more effective than the first approach of playing the largest swing value regardless of sente or gote.

Note that it is very important here to realize, again, that sente depends on the size of the follow-up. If the follow-up to a sente move is smaller than the biggest gote move, then it is not truly sente!

Moves that are sente only when the follow-up is large enough are not sente yet when there is a larger gote move. This means that we can keep moves that are not sente yet in reserve for when they become sente. So we play moves that are currently sente first, but if there is a gote move which is worth more than the follow-up of an ignored sente move, then that comes first.

Next we will look in more detail at the effect of sente, gote and follow-ups on the value of moves.

Average gain (miai counting)

Note: you may find it useful to watch the Kyle Blocher's lecture on Miai counting before reading any of this.

Since it may be difficult to judge if a move is sente or gote - see "What is Sente?" - to adjust the swing value, we could also take a look at the difference in the number of stones played to achieve the swing value. If a move is gote for us, we will have to invest 1 stone more than the opponent in order to reach the end position. This means we invest 1 stone to get our points. If the move is also gote for the opponent, then they would also invest one stone to get the endgame points. So the difference is two stones. This total, of black investment and white investment combined, is called the local tally. So in simple double gote, the tally is two, in sente or reverse sente it is one, and in double sente it is zero.

If we divide the swing value by the local tally, we get a value which indicates how much was gained, on average, per stone. Instead of trying to judge the "sente-ness" of the move, we can calculate scores for different variations, including playing elsewhere, each time dividing by the local tally and find a maximum among the variations. This way of counting is known as miai counting.

Value of a position (the count)

To be able to use miai counting, we also need to know the value of a position, which is an average value of local endgame outcomes.

Lets take a look at a simple example:

Initial position

Black plays first

White plays first

Here, we have a simple gote position. What is the count in this position? The count is the average value of the position. If black plays first, black makes one point locally, marked . If white plays first, no point is made there. We may take the average value, 0.5, as an estimate of the value of the position.

But the count is more than just an estimate. To see why, here is the combination of two of such positions.

Combination  

The points, "a" and "b" are miai. Because of the miai, we may regard the Black territory in the combination as exactly 1 point. Black may guarantee at least 1 point (for Black), and White may guarantee at most 1 point for Black.

White first  

If White plays first in one of the positions Black can play in the other to guarantee 1 point, marked.

Black first  

If Black plays first in one of the positions White can play in the other to hold Black to 1 point, marked.

Since the two positions add up to exactly 1 point of territory (for Black), each has 0.5 point of territory, on average. The count is not just an estimate. Two estimates add up to another estimate, not an exact value.

[edit]

The miai value of moves

Endgame position  

In this corner, there are four endgame moves left, a through d. Each of them is exactly the same.

Since the count (remember: average value) of each of these is 0.5 points for black, this means that with four of them, the count is 2.

The local tally for each of them is two (one more black play if black plays first, plus one more white play if white plays first), and since the swing value is 1, this means that the average gain, per stone is 0.5 points.

Lets see if that is correct.

Four moves later  

Here Black has made four moves locally, and has thereby scored 4 points (the marked intersections). Since the initial count was 2, and each play was said to gain 0.5, the result is consistent with our calculated miai value for these moves.

Four moves later  

Here's the same position, but this time Black played three times and White played once. From the initial 2 points, Black has gained 1.5 and White 0.5, for a net gain of 1 to Black. The result is three points, which is what we observe (the three marked points).

[edit]

What this means for the order of moves

Armed with this new knowledge, we can take another step at determining the correct order for endgame moves. Given the average gain (miai value) of all moves, we could play them in order from largest to smallest.

What does this mean for our earlier approximation of playing in the order double sente, sente, reverse sente, gote?

We can immediately notice that this order has a declining local tally. Double sente moves have a local tally of zero, sente and reverse sente have a local tally of one, and double gote has a local tally of two.

Since determining the miai value of moves involves dividing by the local tally, what does that give us?

Well, for double sente moves we're dividing by zero, which is a strange thing to do, according to mathematics. Effectively we can say that because of the division by zero, the value of a double sente move is infinite. So always play double sente moves immediately!

We can also see that both sente and reverse sente have a local tally of one. This means that playing a sente move or preventing one of the opponent are equally valuable.

Finally, since double gote moves have a local tally of two, we can give the rule of thumb: sente moves are worth twice as much as gote moves.

Note that this is still only a rule of thumb, because we need to take the value of the follow-up of sente moves into account. Lets see if our new knowledge of count, local tally and miai values can give us fresh ideas on this concept.

[edit]

Evaluating branches

Initial position  

Earlier, we showed that this position has a count of 0.5 (it is worth 0.5 points to Black, on average), and playing in it has a miai value of 0.5, since it gains 0.5, making the value of the position either 0 or 1.

Initial position  

Next, lets look at this position. What is the value here?

Black gets 2 points

Black gets 1 point

Black gets no points

Here's three ways in which the position can play out. Black gets either two, one, or zero points here. But not every one of these variations is equally likely, so how do we calculate the average value?

Here, our knowledge of the earlier position comes to the rescue. Lets consider two positions:

Black plays first

White plays first

If black plays first, black gets 2 points. This is easy and straightforward. But what if white plays first? Well, the position after is equivalent to the position we showed earlier. So when white plays first, the resulting position is worth 0.5 for Black on average.

So now we have two positions with exact values. One is worth 2 points, the other is worth 0.5 points. That means that the initial position is worth, on average 1.25 points. The count is 1.25 points.

So what is the miai value of a move here? Well, given that the count is 1.25, and Black can move to a position with a count of 2 using one move, that move is worth 0.75 points. Similarly, white can move from a position worth 1.25 points to a position worth 0.5 points, which also gains White 0.75 points.

Exercise:

Initial position  

Given the above knowledge, can you show what the count (average value) of this position is? Can you show how much a move by black or white is worth? (miai value). Answer

[edit]

See also

• Endgame Tesuji
• Endgame Problems
• Endgame Questions

[1] From Toshiro Kageyama: Lessons in the Fundamentals of Go
[2] Answer to the exercise: The swing value is 9 points (eight points lost plus one prisoner).
[3] Answer to the exercise: Black first gives a position worth 3 points, White first is the position from above worth 1.25 on average. So the position is worth 2 1/8 (=4.25/2) on average. A move by black or white is worth 7/8 of a point.

Question:

I do not understand any of this. Where does the 7/8 come from? Should not it be 2.125/2? And where does 0.75 come from? Impossible to understand.

Answer:

The average gain for a move is the difference between the value of original position and the value of the resulting position. Here, the value of the position is 2.125 (or 2 1/8). If Black plays first, the value becomes 3, which gives us 3 - 2 1/8 = 7/8 gain for Black. Equivalently, if White plays first, he gains 2 1/8 - 1 1/4 = 7/8. For more, see miai value.