TenThousandYearKo/complex example

Again, white cannot fill the ko because he would die. Also, he does not want to start the ko, because if he does, black gets to take first. (White also cannot crush the ko, since he only has one outside liberty.)

Note that here white has an extra liberties outside, which is quite common in a mannenko shape. The one extra liberty will not help white win the ko, but because it takes black 3 moves to properly remove that liberty, it is extremely difficult for black to start the ko. (See next diagram.)

In this position the result is almost certainly a seki.

If black starts the ko, white gets four moves elsewhere, and still gets to take first in the ko. Even if black wins the ko, white will get 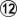and 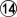as further compensation elsewhere.

By starting the ko, black can (at best, if he can win the ko while responding to all white threats) kill all the white stones in the corner, to a gain of around 20 points (when compared to the likely seki result).

Therefore, even in the optimum case, it is very unlikely that black would want to start the ko, because the 20 point gain from 6 moves is way too small, at least until the very late endgame.

In the late endgame white will have to remove black's threats of more than 8 points (white can ignore smaller ones, as he gains 4 black prisoners by winning the ko), but luckily he will have at least four moves (, , and ) to do so.

This makes it very likely indeed that black's best strategy will be to choose the seki variation.

On the usual assumption that the left side is Black territory, White has a sente with - . Later Black will take and fill the ko, for seki.

elsewhere. fills at .

As usual with hyperactive kos, the koloser starts the ko. As unkx80 points out, filling with hides a ko. continues as koloser.

elsewhere. fills and wins the ko.

White gives up the ko in exchange for 2 moves elsewhere. Counting the two marked points, Black gets 27 points in 2 net moves.

, elsewhere.

White gets 5 points in 2 net moves.

Thus the count of the original position is 11 points for Black, and each move gains 8 points, on average, by territory scoring.

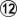, , , , , pass. fills at . 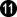at "a".

If White waits until the end of play, then Black will take the corner in 6 net plays, as anonymous indicates above. The type of scoring matters. By area scoring the result is the same as if Black kills the corner in 2 net plays, but by territory scoring it makes a difference of 4 points, and Black gets only 23 points.

OC, this is worse for White than 11 points, which is why White starts the ko in order to force Black to win it while White gains 16 points elsewhere. :)

, elsewhere.

When White is komaster he can take away Black's two points on the left side with - . The play in a real game would be a bit more complicated than the diagram shows. White would play elsewhere, and then Black would start the ko to force White to win it. That ko fight is telescoped, since the local result is the same as in the diagram.

In 2 net plays White gets 5 points.

saves the marked points. The double ko nullifies White's komaster advantage to the extent that Black has a sente after .

elsewhere. fills at .

effectively wins that ko. If White takes it back, Black can take the ko in the corner. Again, the diagram telescopes the ko fight.

In one net play Black gets 3 points while White gets 5, for a net local score of 2 points for White. The difference between this result and when White plays first is 3 points, and the net difference in plays is 3 moves, so each play gains, on average, 1 point. The original position is worth 3 points for White.

In a real game, neither player may be komaster, but the ko is still lopsided, and so Black will probably have the advantage, as he has less at stake. Waiting until the end of the game to make seki will then not be good for Black, and so Black will initiate the ko fight at some point.

Bass: I kinda disagree with the conclusion. For white to be able to initiate the ko, he must be komaster, which is extremely rare (once in a thousand years, approx.) in this kind of lopsided ko, where white's gain will be minimal if he wins the ko. On the other hand, for black to start the ko, it is not enough that he is the komaster, he must be a komonster. Also, black must first spend three moves on the outside, so it is even less likely that black will start the ko. Instead black will wait to the endgame, take the outside ko at his own leisure, watch as white removes black's ko threats (typically losing a point or two while doing so), and when everything else is played out, black gets a prisoner in the corner while making the seki.

Bill: The situation where neither player is komaster is not well defined. Unlike most regular go positions, the distribution and type of ko threats are quite varied, and cannot obviously be characterized by a few simple plays. That said, Black does not have to be komaster to start the ko, or to profit from the lopsidedness of the ko. Your seki scenario, for example, has White losing points in order to eliminate Black ko threats.

Here is an indication of how Black can profit, even when he is not komaster.

elsewhere.

In this position, suppose that Black has another large enough ko threat so that it does White no good to eliminate a threat with . Also suppose that Black's ko threats are matched by White threats, so that the ko threat situation is even.

In the no threat case Black makes seki and gets 1 point for the stone, but White gets 14 points in the other corner, for a net of -13 (13 points for White). In this situation, which is even aside from the ko, White gets 7 points in the ko while Black gets 2 points in the other corner, for a net of -5. That is 8 points better than the seki.

When Black has to start this ko depends on a number of things, but it is possible that he can wait until the end of play. The later Black has to play from this position, the earlier he can play from the original position. A fairly typical scenario, I think, would be for Black to do that when other plays gain 2 points or so.

Bass: I agree that the situation with no komaster is not well-defined as such. However, it is possible to define limits, or a corridor, so to say, that leads to the seki variation being best for both. The corridor is defined by the value of remaining endgame elsewhere, the number and size of ko threats, and the price white has to pay while removing black's threats.

The actual values are tedious to read out, but here are my offhand guesses: As long as there is endgame worth more than killing the corner or white taking the prisoners (guess: around 3 to 5 points per move in each case), then the game is still "in the corridor". When the endgame is getting small enough, then the corridor becomes more and more defined by the ko threat situation, which has to stay between the extreme cases of "black has 4 more threats (with black threat size being 9+ points and white threat size being around 20 points)" and "white has more 20 point threats than black has 8 point threats". (modulo any errors in the actual point values caused by white's need to remove threats, and my being lazy and making mistakes :-)

White the exact limits of the corridor may be a bit fuzzy here, it is clear that the corridor is much wider than that of the other mannenko example. Or in other words: this situation is much more likely to end up as seki.

Bill: OC, it is hard to say anything definitive. However, my impression is that, despite the outside dame situation and possible double ko, as long as Black has ko threats around the size in the diagram or bigger, Black should have a definite advantage.