rubilia/NormalValues
Introduction
I am going to translate this copy of Miai values list to reduced chinese value vectors. Lacking a better name, I will refer to them as "Normal values" for now.
I don't know if this deal is interesting to others at all, but to me, japanese mean and miai values are a little awkward to handle, since I am used to (and prefer) chinese scoring. Under area scoring, captures are irrelevant, so we can identify score points with board points zi (or zĭ) as they are conquered (or shared) by the colors. This allows to visualize normal values directly on the board in a comprehensible way.
The structure of a normal value N is
N (T) = (S, U)
where
- S - "score"
- is the chinese [10] mean value of the current position, as compared to "zero",
- U - "urgency"
- is the jiàn hé value [11] of the current position, and
- T - "tenuki value"
- is the gain currently feasible by playing elsewhere [12].
Note: Like in miai counting, it's assumed that
- there is no absent (super)ko
- the tenuki value is sufficiently stable
- the environment is sufficiently rich, i. e. there is a large number of alternative plays at any given tenuki value.
If you`re used to miai values, you may find the following conversions convenient:
Let Sj be the japanese score, Uj the miai value, tl the initial local move tally and Sref the chinese score of the reference shown above the actual position (making (S+Sref) the absolute chinese score). Then
Sj/moku ≈ tl - 2 *(S+Sref)/zi Uj/moku ≈ -1 + 2 * U/zi
[10] referring to board points (子 "zĭ" - literally "stones"). At the end of the game, each point of the board counts to the color which is agreed to have conquered it.
[11] "Chinese miai value" would be kind of an etymological oxymoron, so I think it makes sense to use the chinese term, jiàn hé. This also allows to implicitely distinguish japanese miai values from what I am calculating here. Anyway, "urgency" refers to the locally biggest plays, regardless of (super)ko restrictions.
[12] I don't really like the term temperature, unfortunately regularly used in combinatorial game theory, because the inherently stressed analogy to thermodynamical temperature is pronouncedly superficial and potentially gets in the way of future informational entropy analysis of Go.
Conventions
- All examples are framed by concealed areas. There are no alternative plays in the frame, and all stones that touch the concealed area are alive.
- The upper part of each board shows "zero", that is, the arbitrarily chosen (0, 0) reference situation (upset).
- In unison with Taoist philosophy, Black (yin) is regarded as negative, right, whilst White (yang) as positive, left.
- Note: In mathematical Go, colors are often associated inversly.
The list below shows the normal values N(T) = (S, U) for T = U, ordered by increasing U.
Beside each diagram you can see the underlying tree of normal values. Steps to the left are White's optimal moves, steps to the right are Black's. In ko situations, covering move alternatives are given, too. Double edges are "forced" answers, being more urgent than the last preceding single edge. Triple edges are same referring to a double edge, and so on for higher sente levels. Equal values of similar positions may be merged.
Linking to the relevant followers is a nice idea, but much work, so I'll do that later.
Reference Section
0.00
(0, 0)
/ \
(0, 0) (0, 0)
Of course, this makes sense only with single-stone self-capture allowed (equivalent to passing).
Bill: Why isn't the score -6?
blubb: Welcome here. Have you read the introduction? :) The distinct upper side of each diagram isn`t part of the actual position but shows the arbitrarily chosen (0,0) reference position the lower side is compared against. Here, the latter is exactly 0 zi better for White than the former, so that`s the score.
Bill: Thanks. :-) You might consider making the reference position the number of stones of each color in the lower side. That will make things more familiar for new readers who are not used to area scoring.
blubb: Isn`t that the case here, except for the eye where in the lower side a stone is missing?
(later:) Oh, perhaps you were thinking of something different. Amongst all the arbitrary choices, I can see three special references (modulo score invariant board rearrangements):
(1) the natural zero, i. e. the empty (or equally devided) board,
(2) the statical "as is", with all stones considered alive,
(3) the one that makes the score closest to zero,
of which I am mostly using the third here. Maybe you are suggesting the first instead?
I have made an illustration of these variants here.
0.50
(0, 1/2)
/ \
(4/3, 2/3)__(2/3, 2/3) (-1/2, 1/2)
// \\ / \
(2, 0) (0, 0) (-1, 0)
w can be regarded as 100% white, and unlike in a ko situation, not just b but also  as 100% black.
as 100% black.
(0, 1/2)
/ \
(1, 1) (-1/2, 1/2)
/ \\ / \
(2, 1/2) (0, 0) (-1, 0)
/ \
(5/2, 1/2) (4/3, 2/3)__(2/3, 2/3)
/ \ // \
(3, 0) (2, 0) (0, 0)
w is fully white, and  fully black again, no matter how many b are there (which also count entirely for Black, of course).
fully black again, no matter how many b are there (which also count entirely for Black, of course).
(0, 1/2)
/ \
(5/2, 5/2) (-1/2, 1/2)
/ \\ / \
(5, 1/2) (0, 0) (-1, 0)
In situations like this and the previous ones, with exactly one w and at least one b,
- w completely belongs to White, whilst all
 stones, as well as all b points, completely belong to Black, and
stones, as well as all b points, completely belong to Black, and
- the urgency is 1/2, just as with a simple shared point.
Bill: Why isn't the urgency 0?
blubb: By connecting at the left one of the two b points, Black can conquer half of w.
Bill: By the same token, a White atari at w conquers even more.
blubb: That atari is strictly sente (inducing the double edge in the tree), whereas Black`s play is not.
I just realise that this may trigger some confusion, because I am using what I`d call excitation. I guess I`ll better state this explicitely, since it occasionally differs from the "temperature".
I am not even sure if this point is worth the deviation. As far as I can see, it suits as a guide to the best move to the same degree as does "temperature" (i. e. with the same limitations regarding tedomari or (hyper)activity). As of now, I find it more sensible though (see here for the why).
...(0, 1/2)...
/ / \ \
(1/3, 2/3)......══......(-1/3, 2/3)
/ / \ \
/..(1/2, 1/2).. ..(-1/2, 1/2)..\
/ \ / \
(1, 0) (0, 0) (-1, 0)
Here, optimal play depends on who is komaster. Nevertheless, due to its symmetry, the position is not hyperactive (in fact, it`s not even active).
(-1/2, 1/2)
/ \
(0, 1/2) (-11/4, 9/4)
/ \ // \
(1/2, 1/2) (-1/2, 1/2) (-5, 0)
/ \ / \
(1, 0) (0, 0) (-1, 0)
Of these 6 unsettled points, only 1½ belong to Black, who furthermore has a valuable ko threat here.
White`s capture may prevent Black`s threat, but that won`t usually happen before dame filling, since it is worth no more than taking a shared point.
0.67
(1/3, 2/3)__(-1/3, 2/3)
/ \
(1, 0) (-1, 0)
Black has 2/3 points equity in  . We may think of it as 2/3 captured. The remainder is the mean value 1/3 ≈ 0.33 to White's favor (hence positive).
. We may think of it as 2/3 captured. The remainder is the mean value 1/3 ≈ 0.33 to White's favor (hence positive).
Hidden ko
(2/3, 2/3)
/ \
(4/3, 2/3) (-2/3, 4/3)
\ // \
(4/3, 2/3)__(2/3, 2/3) (-2, 0)
/ \
(1, 0) (-1, 0)
We may think of both marked points as 2/3 conquered by Black. The 0.67 mean value results from the remaining third parts of them: 2 * (1/3) = 2/3 ≈ 0.67.
(1/3, 2/3)
/ \
/ \
/ \
(1, 1/2) \
/ \ \
(5/2, 3/2) (1/2, 1/2) \
/ \\ / \ \
(4, 0) (1, 0) (0, 0) (?, ?)
// \
(13/6, 11/6)__(1/3, 2/3) (?, ?)
/ \\ \
(4, 0) (1/3, 2/3)__(-1/3, 2/3)
/ \
(1, 0) (-1, 0)
...........(19/9, 8/9)__(11/9, 8/9)__(1/3, 2/3)
/ / \\ \
(3, 0) (7/3, 2/3)__(5/3, 2/3) (1/3, 2/3)__(-1/3, 2/3)
/ \ / \
(3, 0) (1, 0) (-1, 0)
(1/3, 2/3)
/ \
(1, 1/2) (-1/3, 2/3)
/ \
(5/3, 4/3)__(1/3, 2/3) (-7/6, 5/6)
/ \\ \ // \
(3, 0) (1/3, 2/3)__(-1/3, 2/3) //
/ \ \\
(1, 0) (-1, 0) (-2,0)
Black at a starts a ko, White at a prevents it.
The previous situation is a follower of this one, which is why its graph occurs as subgraph here - look for the "asymmetric ko" line
(5/3, 4/3)__(1/3, 2/3)
and below.
- From now on, subtree values already mentioned above won't necessarily be expanded anymore. Here, the (1, 1/2) - that is, White playing at a - refers to the (0, 1/2) being given as second example in section 0.5, with "zero" shifted by 1 point.
- The black sente sequence on the right, leading to (-2,0), is pruned because the actual values are neither determined by our diagram nor practically relevant. (B hardly will let Black brake through.)
0.75
(-3/4, 3/4)
/ \
(0, 0) (-3/2, 1/2)
Defend or take away potential single-point eye.
Currently, x can be referred to as 1/4 white, 3/4 black.
(-1/4, 3/4)
/ \
(1/2, 1/2) (-1, 1/2)
Either player starting at x.
Here, x can be referred to as 3/4 white, 1/4 black.
(-1/4, 3/4)
/ \
(1/2, 1/2) (-1, 1)
// \
(0, 1) (-2, 0)
/ \\
(1, 0) (-1, 1/2)
As can be seen, the marked black stone doesn't affect the value. Still, x is 3/4 white, 1/4 black.
0.83
..(-1/6, 5/6)..
/ \
(4/3, 2/3)__(2/3, 2/3) (-1, 1/2)
/ \ / \
(2, 0) (0, 0) (0, 1) (-3/2, 3/2)
/ \\
(1, 1) (-1, 0)
/ \
(2, 0) (0, 1/2)
 is completely black, and even 1/6 of x belongs to Black.
is completely black, and even 1/6 of x belongs to Black.
(-1/3, 5/6)
/ \
(1/2, 1/2) (-37/24, 35/24)
// \
(-1/12, 13/12) (-3, 0)
/ \\
(1, 0) (-7/6, 5/6)
As can be seen, the marked stones don't affect the value. Still, x is 2/3 white, 1/3 black.
...(-1/6, 5/6)...
/ \
(4/3, 2/3)__(2/3, 2/3) (-1, 1)....
/ \ // \
(2, 0) (0, 0) (0, 1) (-2, 1/2)
/ \\ / \
(1, 1) (-1, 0) | (-5/2, 1/2)
/ \ \\
(2, 0) (0, 1/2) (-2, 0)
 completely belongs to Black, and even x is 1/6 black.
completely belongs to Black, and even x is 1/6 black.
(-1/3, 5/6)
/ \
(1/2, 1/2) (-49/24, 47/24)
// \
(-1/12, 13/12) (-4, 0)
/ \\
(1, 0) (-7/6, 5/6)
As we can see again, the marked stones don't affect the value. Still, x is 2/3 white, 1/3 black.
1.00
(0, 1)
/ \
(1, 1) (-1, 0)
/ \
(2, 0) (0, 1/2)
- The b point and one of the marked stones belong 100% to Black, the other marked stone is White`s.
(0, 1)
/ \
(1, 1/2) (-1, 1)
/ \
(0, 1) (-2, 1/2)
/ \
(1, 1/2) (-1, 0)
- The w points belong 100% to White, and the b points belong 100% to Black.
..(0, 1)..
/ \
(3/2, 3/2) (-1, 1)....
/ \\ / \
(3, 1/2) (1, 0) | (-2, 1/2)
\\ / \
(-1, 0) | (-5/2, 1/2)
\\
(-2, 0)
In situations like this and the previous one, with at least two w and b points each,
- all w points completely belong to White, whilst the
 stones, regardless of their number, as well as the b points, completely belong to Black, and
stones, regardless of their number, as well as the b points, completely belong to Black, and
- the urgency is 1.
Elementary two-step ko
.........(1, 1).....__(0, 1)__.....(-1, 1)..........
/ / \ \
/..(4/3, 2/3)__(2/3, 2/3) (-2/3, 2/3)__(-4/3, 2/3)..\
/ \ / \
(2, 0) (0, 0) (-2, 0)
1.46
work in progress
O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O���������������* * * BELOW, WORK IN PROGRESS * * * ���������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O�������������������������������������������������������������������
Unsecured ko
(4/3, 4/3)
/ \
| (0, 0)
\\
(4/3, 2/3)
The (4/3, 2/3) result represents the plain (secured) ko after white captured and black countered.
Unsecured two-step ko
......(1, 5/3)__(-2/3, 4/3)...........
/ \\ \
| (-2/3, 2/3)__(-4/3, 2/3)..\
\\ / \
(1, 1) (0, 0) (-2, 0)
The (1, 1) result represents the elementary (secured) two-step ko, where black blocked after the second white capture.
Elementary three-step ko
(4/5, 6/5)__(-2/5, 6/5)__(-8/5, 6/5)__(-14/5, 6/5)
/ / \/ \ \
(2, 0) (2/3, 2/3) (-1, 1)(-1, 1) (-8/3, 2/3) (-4, 0)
Unsecured three-step ko
.........(4/5, 9/5)__(-1, 5/3)__(-8/3, 4/3)
/ \\/ \\ \
| / \\ (-8/3, 2/3) (-4, 0)
\\ (-2/3, 4/3) (-1, 1)
(4/5, 6/5)
The (4/5, 6/5) represents the elementary (secured) three-step ko with black having blocked after the third white capture.
.......(-2, 1).......
/ \
(-1, 1) |
/ \ //
(1/3, 4/3) (-2, 0) (-5/3, 4/3)
\\
(-3, 0)
Second line mutual atari
(-3, 1)
/ \
| (-4, 1)
\\ / \
(-3, 1/2) |
//
(-4, 1)
/ \
(-3, 1/2) (-5, 0)
2 vs. 1 on the second line, uncovered
(-3, 2)
/ \
| (-5, 2)
\\ / \
(-3, 1/2) |
//
(-5, 2)
/ \
(-3, 1/2) |
//
(-5, 0)
3 vs. 1 on the second line
.............(-11/2, 3/2).............
/ \
(-4, 1) |
/ \ //
| (-5, 1) (-11/2, 3/2)
\\ / \ / \
(-4, 1/2) | (-4, 5/6) (-7, 0)
// / \
(-5, 0) | (-29/6, 5/6)
\\ / \
(-4, 1/2) (-17/3, 2/3)
3 vs. 1 on the second line, uncovered
...............(-7, 3)...............
/ \
(-4, 1) |
/ \ //
| (-5, 1) ......(-7, 3)......
\\ / \ / \
(-4, 1/2) | (-4, 1) |
// / \ //
(-5, 0) | (-5, 1) (-7, 0)
\\ / \
(-4, 1/2) |
//
(-5, 0)
4 vs. 1 on the second line
..........(-8, 1).........
/ \
..(-20/3, 5/3).. |
/ \\ :
(-5, 1) (-25/3, 4/3) :
/ \ // \ :
| (-6, 1) (-7, 0) | :
\\ / \ // //
(-5, 1/2) | (-25/3, 2/3) (-23/3, 4/3)
// / \\
(-6, 0) (-19/3, 4/3) (-9, 0)
/ \
(-5, 1) (-23/3, 2/3)
/ \
| (-6, 1)
\\ / \
(-5, 1/2) (-7, 1)
4 vs. 1 on the second line, uncovered
................(-9, 2).............
/ \
...(-7, 2).... |
/ \ //
(-5, 1) | ......(-9, 7/3)......
/ \ // / \\
| (-6, 1) (-7, 0) .(-20/3, 5/3). |
\\ / \ / \ ///
(-5, 1/2) | (-5, 1) (-25/3, 4/3) (-9, 0)
// / \ / \
(-6, 0) | (-6, 1) (-7, 0) |
\\ / \ //
(-5, 1/2) (-7, 1) (-25/3, 2/3)
...............(-7, 3)...............
/ \
(-5, 1) |
/ \ //
| (-6, 1) ......(-7, 2)......
\\ / \ / \
(-5, 1/2) | (-5, 1) |
// / \ //
(-6, 0) | (-6, 1) (-7, 0)
\\ / \
(-5, 1/2) |
//
(-6, 0)
.......(-7, 3).......
/ \
(-4, 1) |
/ \ //
| (-5, 1) (-7, 3)
\\ / \ \
(-4, 1/2) | |
// //
(-5, 0) (-7, 0)
.......(-5, 1)........
/ \
(-4, 1) ................(-6, 1).......
/ \ / \
| (-5, 1) |
\\ / \ //
(-4, 1/2) | (-71/12, 13/12)
// / \\
(-5, 0) (-29/6, 5/6) (-7, 0)
/ \
(-4, 1/2) (-17/3, 2/3)
quarry
O������������������������������������������������������������������� O������������������������������������������������������������������� O������������������������������������������������������������������� O�������������������������������������������������������������������
Initial count: -2.5
After  the corner is worth -2. Black has captured 3 White stones, but White can claim the
the corner is worth -2. Black has captured 3 White stones, but White can claim the 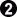 stone.
stone.
(Note: If Black is komaster she can make ko to protect 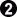 , but White gets 3 moves elsewhere.)
, but White gets 3 moves elsewhere.)
__ horizontal line (for ko): __
═ horizontal double line: ═
![[Diagram]](diagrams/12/621570676f85568ceff18a5e767e401c.png)
![[Diagram]](diagrams/36/874c878baba262f0ee282e3b02d299f3.png)
![[Diagram]](diagrams/14/8c9e3f3163458be64d197d06806af9d1.png)
![[Diagram]](diagrams/20/2e64a27a3f67d5fb5df6480585d9111d.png)
![[Diagram]](diagrams/3/a06ad5e97106f5b323f67c65d4c861c6.png)
![[Diagram]](diagrams/33/946d25fb49c55d1ebef460fe96acc95d.png)
![[Diagram]](diagrams/39/3bf4505a18b33706ae1a2d7007dde2aa.png)
![[Diagram]](diagrams/8/ee1788874f627d4f4d5e3bb804fa951a.png)
![[Diagram]](diagrams/26/2bbd0a429e22a30043875594dcf64f68.png)
![[Diagram]](diagrams/34/e714e8e88f8cac6042385056fc00c614.png)
![[Diagram]](diagrams/3/c34ba08cb8bfc12c8c03edff114b7139.png)
![[Diagram]](diagrams/14/77b2059d2b4b976e68a5e390cea10963.png)
![[Diagram]](diagrams/13/768510e2ebfaf303d9d8539ef702d838.png)
![[Diagram]](diagrams/3/5a4048c9c8b8cea46f059ba384d03e16.png)
![[Diagram]](diagrams/47/376faad98c5b8ed864c9cd36e964d9fa.png)
![[Diagram]](diagrams/21/d769a25e941982fde167009975daa1e2.png)
![[Diagram]](diagrams/40/39b3083478592cabfcdbb36d43b8f169.png)
![[Diagram]](diagrams/22/e01a22fa1a8742e729f561e710c684e8.png)
![[Diagram]](diagrams/52/3ac288721ccdfc30dea63b39ba84a45c.png)
![[Diagram]](diagrams/0/8da26f9aa27d399e8f38bb1392125b56.png)
![[Diagram]](diagrams/2/6c7f78cbed12638bd3d1963d28d6e7bd.png)
![[Diagram]](diagrams/12/932664bda20131ff7087f0cab6af435b.png)
![[Diagram]](diagrams/18/d80db4bca7d8c0bddf49310fc7f4f523.png)
![[Diagram]](diagrams/45/8427a12103aaad516cd98b29efecec21.png)
![[Diagram]](diagrams/16/0c68734e9659db4440819cc367389285.png)
![[Diagram]](diagrams/5/9aedd8e378317bfa467419c9ec48480c.png)
![[Diagram]](diagrams/35/7da05d94dc1d68b250f90430dacde542.png)
![[Diagram]](diagrams/25/5d582926bb01183f97db99506562fad5.png)
![[Diagram]](diagrams/27/7b674db286836655234b04142868a129.png)
![[Diagram]](diagrams/5/92a5b74eb5d5606dec1f4ce27e9df7d6.png)
![[Diagram]](diagrams/7/c9e11295d693117d9e7be3e95fd1e97e.png)
![[Diagram]](diagrams/41/b8c6bf6ffe11eacd4ebed69843fc585e.png)
![[Diagram]](diagrams/44/2b2abb412247f7120c1d62236d5ff12a.png)
![[Diagram]](diagrams/23/6210c853a4c6dbaa70af4db5377bce54.png)
![[Diagram]](diagrams/45/951bd2c9dbe8e44536a5e13c22269f8e.png)
![[Diagram]](diagrams/9/8ab07c943854407d2f29cf1fd4bcb11b.png)
![[Diagram]](diagrams/32/fc9ec35adb3c2db3c90842f507d91717.png)
![[Diagram]](diagrams/12/6f21f85756cc53614de97cd9304ef717.png)
![[Diagram]](diagrams/42/41f08af7b81aaa574a1ce2fb98a0d408.png)
![[Diagram]](diagrams/7/c62171fb5bc716135c2134823599ff0f.png)
![[Diagram]](diagrams/42/54b0b6edfeee19a55b256199dcc1ed4a.png)
![[Diagram]](diagrams/6/b8b3c95756fa22a80f4db6a57772830c.png)
![[Diagram]](diagrams/33/eade2c48e163d6c60d1c783176610323.png)
![[Diagram]](diagrams/29/cfe74e42ff0e47f29a48c04071379356.png)
![[Diagram]](diagrams/29/78c0682c3543e70a52716dce3972c031.png)
![[Diagram]](diagrams/49/8c5bfab9bf7ffb181966aa03bef3eb37.png)
![[Diagram]](diagrams/10/a69bed6076c5b4d7ed848891bd81e44b.png)
 Black gets 2 White stones plus 1 point of territory.
Black gets 2 White stones plus 1 point of territory.
![[Diagram]](diagrams/13/0a519340dd06f8a3166169d2ab1a7be9.png)
![[Diagram]](diagrams/52/bae933d2919dc4f2f7c308dbe6e181f5.png)
![[Diagram]](diagrams/41/b2670344555923ea9b7ea4e63eb3cafd.png)
![[Diagram]](diagrams/45/58e6e9f2d1b7bfa3296a388db85df8ed.png)
![[Diagram]](diagrams/23/0ca0ee8d7df2f319e331ce5de8b14d19.png)
![[Diagram]](diagrams/29/7b649c2dc6539a12f1f8b38746ddb762.png)
![[Diagram]](diagrams/50/24879c1bedc6d3c3a9992dc71d4b1cf8.png)
![[Diagram]](diagrams/24/f10cb8321c657a732cd3585def8fbafe.png)
![[Diagram]](diagrams/4/31430cd33f976c5ddc616f5f2a8c18f2.png)
![[Diagram]](diagrams/14/635d994ff90bffb52d0488978b2c3330.png)
![[Diagram]](diagrams/12/b8d5b0e123b7333ddd372913dfb24f25.png)
![[Diagram]](diagrams/28/2605fa7c2e25013d86735836a06488f0.png)
![[Diagram]](diagrams/26/d7cb1856bbac67d644ba472913d64150.png)
![[Diagram]](diagrams/15/2138a59e4d12504ad77faf3eb83c7c39.png)
![[Diagram]](diagrams/9/4f7082bedae9c037d370d61367b22c60.png)
![[Diagram]](diagrams/23/9ed69603c043853d70730b50b250b862.png)
![[Diagram]](diagrams/28/f8d3078aeee530dc6639002c659f90c3.png)
![[Diagram]](diagrams/13/7c0b20b2e9cc45e4ced8612a916a936d.png)
![[Diagram]](diagrams/25/fcb1adcaa00345a3304ecec38a9a315e.png)
![[Diagram]](diagrams/20/1c2f2ed01c976f9bbb43e1c98df81cd8.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)