MostDifficultProblemEver/Shuko's Solution

Solution 1-10  

threatens to capture the lower right white group in an oiotoshi with a move at a. prevents this, after which connects to prevent white from capturing two black stones and connecting her groups

With through , white defends her group on the right while attack black there. through prevent white from connecting, but must allow the cut

Solution 11-20  

With , white prevents the black group on the right from connecting. is atari, giving black sente. With through , black destroys white's eyeshape, making a temporary seki between the two groups on the right.

This seki will only last if the white group in the lower right corner does not die. As it cannot live independently, white must try to prevent black from forming two eyes in the lower right.

Solution 21-30  

With , black threatens to make two eyes for his group. does the same for the white group in the lower right, and with and 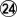, both players prevent the opponent from making two eyes. Thus, for now, another seki is born, this time between the groups in the lower right.

With 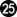through 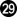, black starts an attempt to escape. White cannot block black, because black would then capture at a. And if black captures, white must play at 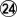again to prevent black from living. But after each of the moves 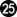, 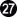and 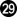, white would not have time to play at 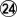because she would get cut (at 26, 28 and 30 respectively. White has no choice but to comply with blacks escape, falling back constantly so as not to give black any opportunities.

Solution 31-40  

With 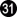through 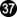, black continues the pattern. On each move, white is unable to black, because she would not have time to play if black captures at a.

With 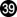black stubbornly keeps walking out, because escape would mean the death of the white group in the lower right, and since that would also lift the seki on the right, it would make most of the right side black territory. White has no choice but to keep chasing black with

Solution 41-50  

Black keeps running, and white keeps chasing him. Allowing black to bend to the left would means escape or death. This is because a is still sente for black, requiring a response at . But after that, black would cut in the center and then play b, which kills to white group at the bottom.

Solution 51-60  

With , and , black again threatens to cut, and white is forced to defend. White cannot allow black to capture at either, because this would result in a ko that white cannot win. Thus the chase continues.

Solution 61-70  

and are stunning moves. The entire central black chain is in atari! Why does black cut? Why doesn't white capture? It turns out that the situation is a rare example of a hanezeki position. If white captures at a, and black takes back at , then white must play to prevent black from forming two eyes. But the exchange has given black the single extra liberty he so desperately needs to lift the seki in the lower right.

So white is left with no other option than to leave the black chain on the board. But after , white is cut, and so must live at the bottom with .

With , and , black shifts his attack to the white group on the left. Capturing these would connect the central black chain to the left.

Why white cannot capture [see diagram to the right]

If white takes the central chain (at ), black will take back at . White must play , but with , black starts approaching the group on the right. After , white is in atari and must capture with . is at , and after the exchange, white is one liberty short.