Klein Bottle
Go can be played on mathematical surfaces called ![[ext]](images/extlink.gif) Klein bottles. This is one of the possibilities for EdgelessGo.
Klein bottles. This is one of the possibilities for EdgelessGo.
One simple way is the 'flat' Klein Bottle: take a normal goban of any size, and consider the edges to wrap around, somewhat like in ToroidalGo. The left edge wraps to the point on the same row on the right edge, but the top edge wraps to the point on the bottom edge on the opposite column. (In ToroidalGo it wraps to the same column.) Allegedly the defunct BasiliskGoServer supported this.
Here is a diagram for 7×7. There are 49 intersections (13 with labels surrounding 6×6 without label), and they all have 4 liberties. They also all have 4 diagonal points, so this is also a 'local grid' board, as described on the EdgelessGo page.
There are other possibilities which have different geometries, but the same Klein bottle 'topology', listed below.
Mathematical stuff

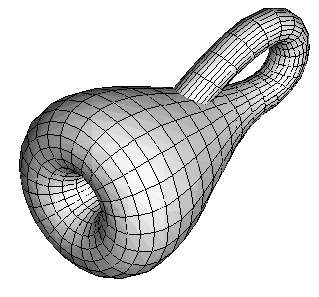
A Klein bottle is a ![[ext]](images/extlink.gif) non-orientable surface[1], where there is no distinction between inside and outside. So unlike a sphere, where you cannot pass from the outside to the inside without passing through the surface, in a Klein bottle you can do just that. If you were very small, an ant say, you could start at any point, and keep crawling until you reached the other side of the surface, without passing through any surfaces, and without needing to cross any edges.
non-orientable surface[1], where there is no distinction between inside and outside. So unlike a sphere, where you cannot pass from the outside to the inside without passing through the surface, in a Klein bottle you can do just that. If you were very small, an ant say, you could start at any point, and keep crawling until you reached the other side of the surface, without passing through any surfaces, and without needing to cross any edges.
It was first described by the German mathematician Felix Klein in 1882, and it is related to the Möbius strip. 
Essentially he combined two Möbius surfaces, a left and a right, to form a single surfaced 3 dimensional object. Although in fact a Klein Bottle is really a four dimensional object, that is immersed in three dimensions.


The Science Museum in London has a very unusual exhibit - a triple Klein bottle, one inside the other:

This is one of a series of glass Klein bottles made by Alan Bennett in Bedford, United Kingdom for the Science Museum, London. It consists of three Klein bottles, one inside another.
A Klein bottle is a surface which has no edges, no outside or inside and cannot properly be constructed in three dimensions.
In the series Alan Bennett made Klein bottles analogous to Mobius strips with odd numbers of twists greater than one.
- Image number: 10314758
- Credit: Science Museum/Science & Society Picture Library
- Date taken: 20 October 2003 14:40
- Image rights: Science Museum


Euler Characteristics
When you take a polyhedron and count its faces F, edges E and vertices V, and compute χ = F - E + V
It turns out, closed surfaces are topologically different if they have different Euler characteristics. (By closed surface, we mean a surface without boundary.) The torus has Euler characteristic 0, the pretzel (a torus with two holes) has Euler characteristic -2, and every hole that you add reduces the Euler characteristic by 2. There are also non-orientable closed surfaces; the most famous is the Klein bottle has Euler characteristic 0.
[1] Orientable and non-orientable surfaces: A non-orientable surface does not have a proper inside or outside.

The best known example is the Möbius band. If you put a non-symmetric figure on it, for example the letter R, and slide it over an appropriate loop, then it returns to the original position in mirror image.
The Möbius band has a boundary. This boundary can be is sewn up (in two different ways) to produce non-orientable surfaces (the Klein bottle and the projective plane) without boundary.
A mathematician named Klein
Thought the Möbius strip divine.
Said he, "If you glue
The edges of two
You'll get a weird bottle like mine."

Other possibilities for playing Go on a Klein Bottle
Same label, same intersection.
Note that some points on this board are linked to more than 4 other points (a has 5 neighbours; b has 6, ...); so this board does not meet the second requirement in the definition of Edgeless go.
(fool: In the inner ring, a-b, c-d, e-f, and g-h are NOT supposed to be linked, just like they are not linked in the outer ring. But I don't know how to make that appear in a diagram.)
Here is an modified (and smaller) version of the above, where there are 52 intersections (12 labeled, 40 unlabeled), and they all do have 4 neighbours. (But it is not a 'local grid' board, as defined on the EdgelessGo page. For example, you cannot cross-cut around the point m in the diagram.)
![[Diagram]](diagrams/46/f9109339dfbec2409641bfcb83024764.png)
![[Diagram]](diagrams/46/e0160b3ab8e143d1245582a54859e4fb.png)
![[Diagram]](diagrams/51/45db2f9f518263d4cb5fcc839b54d85b.png)
![[Diagram]](diagrams/11/d0890ac982b2371bd2ed08c03a63312f.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)