Thermograph
The thermograph of a game is a graphical representation of the value of playing in it at different temperatures. The axes of the thermograph are the temperature (vertical) and the count (horizontal). At each temperature, the left wall of the thermograph shows what Left (Black) gets by playing first, and the right wall shows what Right (White) gets by playing first. At high enough temperatures the thermograph is topped by a vertical mast, which coincides with the left and right walls, and represents the count of the game. The temperature at the base of this vertical mast is the temperature of the game. In go it corresponds to miai value.
Example
The following shows an endgame position and the corresponding game tree (left branches correspond to black moves and right branches to white moves):
G
/ \
a/ \
/ \a
H \
/ \ \
b/ \b \
/ \ J
1 0 / \
b/ \b
/ \
K L
/ \ / \
M -1 -3 -5
Diagram 2: Game tree (M: Ko with count 1/3) |
G
/ \
/ \
/ \
0.5 \
/ \ \
/ \ \
/ \ J
1 0 / \
/ \
/ \
-1/3 -4
/ \ / \
1/3 -1 -3 -5
Diagram 3: Game tree, partially evaluated |
In Diagram 3, (preliminary) counts are assigned to positions H, K, L and M. Position G is a sente with miai-value 0.5 - (-1/3) = 5/6, since the threat at J of -1/3 - (-4) = 3 2/3 points is large enough. The count is therefore -1/3. Now let's look at the thermograph for this position (diagram 4).
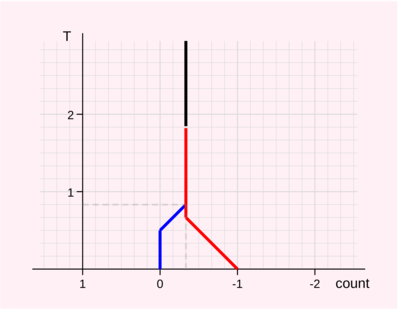
Diagram 4: Thermograph for position G
As expected, the vertical mast (black) is at x-position -1/3, indicating the average value/count of the game. It is convention that the count increases to the left. This makes sure that the features associated with black (the blue line in this case) are on the left side, as is custom in game theory. The left and right wall meet at a temperature of 5/6, which corresponds to the miai-value.
Given an endgame like position G, both players would make a certain number of moves, then tenuki when the remaining moves are too small. (And come back later when the temperature has dropped.) The point, at which a player will tenuki, depends on the value of other endgames on the board, i.e. the current temperature. This temperature dependency is encoded in the thermograph. The slope of red and blue lines indicates how many moves each player makes (or rather the difference):
- vertical lines: sente, i.e. both players make the same number of moves before playing elsewhere
- slope of 45 degrees: gote, i.e. the player who moves first makes one more move than the opponent
- slope of 0.5: related to ko (see below)
Let's break down the different temperature ranges:
- T > 1 5/6: For temperatures greater 1 5/6, both players would ignore position G and play for example a ±2 point gote endgame instead.
- 5/6 < T < 1 5/6: The red mast extends all the way up to 1 5/6. This means that in the temperature range from 0.83 to 1.83, it is white's exclusive right, to play the sente at a. Black cannot play the reverse sente at this temperature, i.e. she should prefer to play a simple ±1 point gote endgame over a play at 'a' in position G.
- 2/3 < T < 5/6: Now if the temperature has cooled down to the range from 4/6 to 5/6, the reverse sente is playable for black.
- 0.5 < T < 2/3: In this range, the game is double gote.
- T < 0.5: Now the situation has reversed and the endgame is (sort of) sente for black.
- T = 0: The counts at temperature 0 correspond to the optimal result for black/white when the endgame is played in isolation.
The incentive to play in the position is given by the horizontal distance of the red and blue wall at the current temperature. If multiple endgames are playable at the current temperature, you would choose the one with the greatest incentive.
Generally, it is more common that the endgame will be played near the highest possible temperature, so the miai-value and count is still the most important information. However, some game trees can be complicated and hard to classify as a simple gote or sente. The thermograph is unambiguous and the construction follows a clear procedure. So it is a reliable way to determine the miai-value and count of an engame position.
How to construct a thermograph
To construct a thermograph, start with the thermographs of the positions that arise after a move by black and white. In this case, we need the graphs for position H and J - they are given in diagram 7.

Diagram 7: Thermographs for position H and J side by side
Now each player has to pay a tax for the privilege to make a move (Cooling). A temperature of T means, there are gote plays of miai value T on the board. The question is, how much better is the current endgame, compared to a ±T gote? To answer this, T points are subtracted from the count for a black move and T points are added to the count for white move.
After a black move, it is white's turn, so the tax is applied to the red line and the black mast in the thermograph for position H. (The red line corresponds to the best result for white.) This is indicated as a green line in Diagram 8. Similarly, the tax for the white move is applied to the blue + black line in the thermograph for position J.
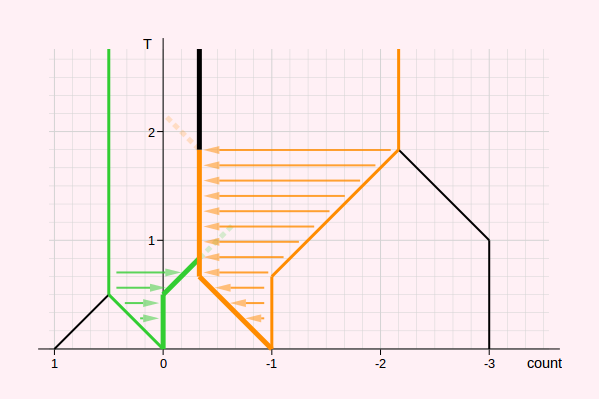
Diagram 8: Constructing the Thermograph for G from the thermographs of H and J
The arrows in Diagram 8 show how the tax is applied. The green line is moved T units to the right and the orange line is moved T units to the left. As a result, the two taxed lines cross or touch at a certain point. From this point, a mast is drawn upwards. Any part of the taxed lines that crosses the mast is disregarded (semi-transparent dashed lines). A taxed line may run "on top" of the black mast a certain distance (until it finally crosses the mast) as seen with the orange line in diagram 8.
The result is the thermograph of position G from diagram 4.
Now how to get the thermographs for position H and J? The procedure is based on the thermograph of a position that is fully played out, with final count c. It is simply given by a black mast at position c.
To verify the thermograph for position H given in diagram 7, draw 2 masts at positions 1 and 0 (the final scores when black/white moves in position H).

Diagram 9: Constructing the Thermograph for position H, a simple gote endgame
Both masts are taxed as indicated by the arrows, resulting in a typical gote thermograph (miai-value: 0.5, count: 0.5).
Ko
A ko complicates the themperature theory. You generally have to make some assumptions about who can win the ko. Then the thermograph will tell you if this is worthwhile in terms of points. Let's look at the ko in position M. It is a minimal ko with swing value 1.
M
/ \
N 0
/ \
1 M
Diagram 11a: Game tree for position M |
M
/ \
* 0
/
1
Diagram 11b: Game tree for position M (no Ko threats) |
From position N, White can move back to M after playing a ko threat. Now let's assume no one has any ko threats. Then the thermograph for position M is constructed based on two masts at counts 1 and 0. The right mast at 0 is taxed normally since white needs one move to finish the ko. However, black has to invest two moves, in order to win the ko, so the mast at 1 is taxed double. The result is shown in diagram 12.
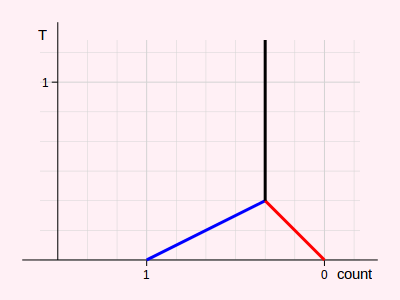
Diagram 12: Thermograph for position M, a 1-point swing value ko
While temperature theory for games without repetitions is well developed, including ko is challenging and an active area of research.
More examples
 Thermograph for example 2: miai value 1 1/12, count: -1 1/12 |
*
/ \
/ \
/ \
/ \
* *
/ \ / \
* -1 * -3
/ \ / \
>2 * -2/3 -2
/ \
* -1
/ \
>2 0
Game tree for example 2 |
The thermograph for example 2 is roughly sente-shaped. Except it has a small gote top. The absence of a colored vertical mast means that both players have the same probability of making the first move.
In addition, there is a double-sente temperature range (T = 4/6...5/6). This corresponds to the situation that after  , black will respond
, black will respond  , but the follow up at a is not big enough yet, so white plays elsewhere.
, but the follow up at a is not big enough yet, so white plays elsewhere.
See also
- Colored mast describes a convention to show when which players may play locally without loss.
- Cooling shows another example of a thermograph.
See existing discussion here under
![[Diagram]](diagrams/52/5fa78ad1c79f32b7f40b2590a6e177ab.png)
![[Diagram]](diagrams/45/a7473d8571d33c1904217752a839f72d.png)
![[Diagram]](diagrams/14/0c88169a9337ec740be309b0b29b3a51.png)
![[Diagram]](diagrams/18/044328becf9f94702031a59d79f3b522.png)
![[Diagram]](diagrams/21/605902ba6d145404fe5dbe6cadc92ebb.png)
![[Diagram]](diagrams/24/d6ea74b27af1b7c236973d3f798e08a5.png)
![[Diagram]](diagrams/39/ed102a2f0686300f5c39b3d9e550eb07.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)