Stable follower
The idea of a stable follower arises when one tries to evaluate the importance of a local position as the difference between Black or White playing there first: it is the first subsequent position to which we can assign a useful value.
One can see this endgame concept in relation with an idealised endgame reckoner.
In order to evaluate an endgame play, one needs to count the difference between the current position and one of known 'count', in both directions (Black to play, White to play). That reference position need not, however, itself be a completely played-out position.
![[Diagram]](diagrams/16/4d37edfdf2d2bb2b9529f6a1d6120670.png)
For example here after 
, there is still another play worth points here: the comparable hane-connect on the first line with Black at a or White at b.
Using a complete enough endgame reckoner, one ought to be able to terminate analyses at such a point, which you could call a stable follower.
Whether one could terminate at the point after White has played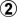 
is another question. In fact it would be useful to do that, and the corresponding position ought to be there in our reckoner, since it is also a common one.
If we imagine that the reckoner is built up (inductively) from the smallest plays, we see that we shouldn't claim as stable follower any intermediate position leaving plays of higher value [1] than we have already dealt with. This confuses the idea of what we are doing with a possible circularity. In terms of SL usage, the page for plays of miai value equal to 3.5 ought only to link to the pages for lower miai value.
To say that better, one can try to use the powerful general notion of reversible play, from CGT.
In terms more familiar to go players, you can say this: use 'fast forward' over parts of the sequence under consideration that are obviously sente, and then stop. This will be your first 'stable follower'.
[1] Bill: Stable follower is a term in thermography. A stable follower must have a smaller miai value than all its ancestors. Stable is defined by Berlekamp in "The economist's view of combinatorial games" in Games of No Chance.
It is true that sometimes it is correct to make a play to a position with the same miai value and leave it temporarily.
![[Welcome to Sensei's Library!]](images/stone-hello.png "Sensei's Library")