19X19 diagram  

The long line of stones is on the board's centerline. This is shown for N=19 but works for any odd value of N>2. If N is even then we can instead begin with this alternate (N+6)-stone pattern:

14X14 diagram  

From then onward, anytime white plays a move (x,y), black responds with the "mirror move" (N+1-x, N+1-y). (I assume the rules are that "suicide is illegal" and x=1,2,3...,N coordinate system.)

If white plays a move which would be illegal for black to mirror -- this can happen if, say, white basically suicides (i.e. makes black capture) a white group above and touching the centerline (the corresponding black below+touching group is not captured) then white moves into his killed area (black cannot because the corresponding area is filled with black stones) -- then black simply passes.

Discussion

It is well known that "mirror go" is not a good strategy in go without any handicap stones, see http://senseis.xmp.net/?Manego and http://senseis.xmp.net/?CounteringMirrorGo . If black tried first moving to the centerpoint then mirroring from then onward, he loses either because of

(i) a shortage of liberties allowing white to capture his central group -- but this cannot happen in my handicap scenario, central group is unconditionally alive.

(ii) or a situation with two converging "ladders" yields the same thing -- also cannot happen in my handicap scenario.

(iii) or one can set up a situation with two "ko"s A and B with mirror images A' and B'. White captures in A, and Black mimics by capturing in A'. Then White captures in B, and Black captures in B'. Then White recaptures in A', and Black recaptures in A. Finally White recaptures in B'. The "superko rule" (repeating position is illegal) forbids Black from recapturing in B, so he has to stop mimicking. -- However, in Japanese go rules, there is no superko rule; instead if a position is repeated that is not merely a simple ko, then if at least one of the players desires, the game is "no result" and is to be re-played or perhaps (if there is not time for replay) regarded as a tie ("jigo") or adjudicated. So I am trying to argue that our handicap strategy yields either a black victory or "no result"/jigo.]

Incidentally, this all is a STRONG ARGUMENT FOR ADOPTING A FORM OF THE SUPERKO RULE in go -- otherwise it would be too easy for a moron to win or draw at handicap go.

(iv) If black in a 10-stone handicap game on an NxN board with N=even were to begin by placing the unconditionally alive handicap-stone group

foo1  

at board center, or in an NxN (N=odd) 11-stone handicap game

foo2  

then mirroring from then onward, that would not work because white could contrive to get an annular situation near the rim of the board like

7x7 diagram  

in this situation, white makes a large capture by playing in the upper right corner, then black would not capture anything playing in bottom left, in fact it would be an illegal suicide.

-- However, again, this "annular" anti-mirror ploy again cannot be used in my N+6 handicap stone scenario.

(v) in a no-handicap game with N=odd if white just tried mirroring black, then black at some well-chosen moment could move to the centerpoint which is a move that cannot be mirrored and which also can be made decisive.

Summary

So does this really constitute a proof? I've just argued that all the usual standard ideas in go for stopping mirror-go from working, do not work against my handicap-go strategy, at least provided we adopt the right rule-set (suicide-illegal, Japanese no-superko rules, and Chinese scoring). It is a much stronger claim than any previous I've seen (all the previous strategies I ever saw needed H to be of order N squared, not order N).

But it seems to me that more generally, we can argue by induction on the number of moves that with this strategy there will be exactly the same stone formation above & below (mirrored & color-reversed) the original eternal handicap stones, except that there can be white groups captured by black, for which the mirror-corresponding black groups stay uncaptured. Hence it really is a proof, i.e. each point of the board has a mate such that the sum of the two is a nonnegative Chinese score for black, so in view of that plus the original N+8 advantage, black must win.

Side note: With minor modifications I think proof should still work even in rules where suicide is legal and/or other-than-Chinese scoring; but the Japanese "superko is no result" rule really does seem essential for my proof. White then could keep repeating, but the point is he cannot break the perpetual repetition to try for a win, without losing.

Another side note: John Tromp (European amateur 2 dan) suggested to me that black fill both the horizontal and vertical centerlines, except for the centerpoint itself, with handicap stones (2N-2 stones; 36 when N=19) and then white would only be able to move first in at most 2 of the resulting 4 quadrants. Black would occupy the (3,3) point in both the quadrants he got to move first in, and then would play to totally prevent white from living in these two quadrants, basically ignoring the other two. Tromp's strategy is not a proof of victory, it is merely an idea for a future proof; but it seems just barely conceivable to us that future computers could genuinely prove it (if it is true) for N=19. But there seems little doubt that Tromp's proposed proof method, even if it can be justified when N=19, cannot possibly be valid for, say, N=51.

fractic: A proof along these lines is not so hard with enough stones. Here is a proof that 54 stones will do.

Warnings

I'm only a 9 kyu (estimated) player here making a claim which was apparently not noticed by players such as Janice Kim, Martin Mueller, and David Fotland (see intro above) all of whom are well over 9 stones stronger than I, so caveat emptor. I'd appreciate any further comments you all have; also you may want to edit the page since this is my first time using the Sensei go wiki system and I've probably formatted things poorly. Can anybody improve the result to reduce H below 25 or to grow sublinearly with N in the limit of large N? (And can this proof be refuted?)

(end.)

Comments

Bass: This is a nice problem (I rememeber solving it some ten years ago), and white can indeed win against this strategy. (The one where the middle line is occupied by unquestionably live black stones, black always mirrors and passes where that is impossible.) You'll have to first create an asymmetry and create a proper shape, and then play "under the stones" to capture while black is passing. The diagrams below will spoil the fun, so try to solve it yourself first.

Counterexample, part 4 ( pass, pass)  

(EDIT: In retrospect, , and 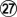and the corresponding black moves are not necessary for white's strategy to work. Since the example works either way, I'll just leave them as they are.)

Counterexample, after part 4  

This is the important point. Now the symmetry is broken so that white has liberties at the points where captured white stones were removed. Black, on the other hand, does not have those liberties, since his stones are still on the board.

Counterexample, result: white wins.  

Now if black attempts to mirror that would actually be an illegal suicide and in many rules an instant forfeit.

Proof probably cannot be rescued?

Warren D. Smith again: After Bass found this refutation, there still remained some question whether the proof could be salvaged. But some further thought mostly by Bass makes us suspect it cannot be salvaged.

The obvious salvage attempt is: black instead of PASSing when white moves to previously-killed white locations (which for black were not killed), instead CONNECTS. Black's goal is to maintain the invariant that for each mirror-pair of vertices, it is either (1) white+black, (2) black+empty, or (3) empty+empty. The problem is there could be black groups which later can be killed in case (2), so black aims to connect those groups to the always-alive component using any "free moves" white offers him. For example Bass had black passing on moves 30 & 32, but black could instead use that opportunity to connect where white had earlier played 1 & 3.

The question then is: is such a connection-to-prevent-future-kill-of-bonus-black-stones always going to be possible? It at first looks like the answer is "yes" because it looks like white always has to offer black as least as many "free moves" as he needs. But unfortunately white can make the connection distance arbitrarily large (on a large enough board).

Further, this proof-rescue idea (even if valid, which it might be) remains pretty inadequate to rescue the proof for the following reason. White can make ARBITRARILY MANY COPIES (if on a large enough board) of such counterexample scenarios (or similar ones; they need not all be identical) like traps waiting to be sprung. Then, when white starts springing them by playing unmirrorable moves, black has to decide WHICH of his "bonus groups" to defend. Even if the defense required always is simple, there are many possible rescue-orderings black could try.

With many mousetrap copies, each with arbitrarily large connect-distance, made before white starts to activate his game plans, and many different mousetrap-types, black having to choose requires some thought, as opposed to being trivially automatic.

As soon as thought is required, it quickly gets too hard to prove anything (at least without a gigantic computer-aided search). The whole goal was to devise a strategy for black which would work without any thought, and that goal seems busted. (I'm not completely convinced it is busted, though, because possibly there is still some "choose which to connect" strategy simple enough to describe, that always works. But I doubt it, so it probably is busted.)

 

dmwit asks: Isn't this a more obvious way to salvage the proof (albeit using more handicap stones)? The fact that white exploits to break symmetry is that the boundary of the board acts as both a solid black wall and a solid white wall based on context. To fix that, have black make a solid black wall using handicap stones. Anyway, the nice thing about this fix is that it still only requires O(n) handicap stones rather than O(n²) stones.

Warren D. Smith again: I doubt dmwit's idea is correct. He(she?) thinks that the reason behind Bass's refutation of my original "proof" was the boundary of the board. But I do not think that was the reason; I think Bass's refutation ideas can be made to work in a boundaryless setting.

ThorAvaTahr: I think I agree with Warren. I think that the trick for refutation of the original problem lies in symmetry breaking and the walls are the cause of symmetry breaking. This is much like ordinary field theory in physics, perfectly symmetrical until you apply boundary conditions. In the proposition of dmwit, the boundary conditions are still applied, only they are forced to be favorable for black. But it is still possible to force black to break the symmetry. It seems the only way to keep symmetry is by playing on two separate boards.

Symmetry broken, black loses as it cannot copy white's move inside the eye  

New idea (of no practical, but mathematical) interest for large N

Warren D. Smith again: My original idea (if it had worked) would yield H=N+6. The ideas which genuinely work, all have H growing quadratically with N, which is pretty pathetic.

I will now outline an idea, which should for enormous boardsizes N, yield H growing slightly slower than quadratic, namely H=constant*N*N/SquareRoot(logN) handicap stones should suffice! (In this section we shall use superko rules.) This is going to be completely crazy for all practical purposes, it is purely to demonstrate there is a short mathematical proof that a subquadratic number of handicap stones suffice!

The handicap player makes a 'wireframe grid' with grid-square sidelength of order SquareRoot?(log(N)). Now, within each grid square, play proceeds. Now there are only 3 to the power X possible goban positions within a grid square with X initially empty locations. Hence, the proposed handicap grid pattern contains enough grid squares, each small enough, so that it would be possible to play every possible goban position, one in each grid square (call those the 'exploratory' grid squares), and still with an arbitrarily large constant fraction of grid squares left over (call those the 'money' grid squares)!

So the handicap player simply adopts the strategy of trying every possible strategy, in the exploratory grid squares. He keeps track of which ones work. Then he re-uses the working ones, in the money grid squares. (which grid squares are 'exploratory' and which are 'money' is not fixed, and the handicap player can change his mind about that assignment as play proceeds. The point is, somewhere the strong player is forced to show the handicap player how to win in a grid square versus any strategy, he has no choice, and then the handicap player can re-use that knowledge.)