MonkeyJump/And Ko

1sj start --- cont'd.....  

Black has 2 ko threats at 'u' and 'v' ('u' is the larger), whilst White has none. Once (a one-space-jump) is played, then , & follow. White must then decide between at 'z' if she wants ko, or at 'y' if she doesn't.

White wants ko.

W chooses 'z'.  

If White plays at 'z', Black must play at 'y', and 5 - 7 then follow. 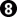makes the larger ko threat.

White now has the option of sequences (a), and (b). The best one for White depends on the size of Black's threats, and the value of sente.

Sequence 'a'.  

carries out the larger threat.

Sequence 'b'.  

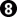answers the larger threat. at 'x' prevents Black filling the ko, and is effectively an internal threat. makes the smaller threat. at 'x' wins the ko. carries out the smaller threat. fills to the right of 'x'.

White doesn't want ko.

W chooses 'y'.  

Relevant sequences are shown for a narrower, but very similar position, at goproblems.com in problems 3844, 4857 and 5781; the feedback from which formed the basis of this discussion. The top left interface is also slightly different causing a small variation in threat size requirements, but the overall argument is the same.

What is sufficient ko threat advantage? White does not need threat advantage, as she takes first in the ko. It is Black's threat advantage that is determining. With only one Black ko threat, however large, a one-space-jump is never better than a large monkey jump. This is because White can save the threat AND win the ko, by playing x after Black retakes.

The minimum requirement for the one-space-jump to be better than a large monkey jump is 2 threats. When sente is worth nothing, the smallest threat sizes that work are 15 and 11. The maximum gain Black can get by choosing a large monkey jump is 2 points.

In summary: With this formation in a real situation, it will be very unlikely for an one-space-jump to be superior to a large monkey jump. The maximum advantage Black can get is only 2 points, and to realise this he must have 2 more large threats than White, and risk fighting a difficult ko. On the other hand, the best defence against a large monkey jump into this formation is very poorly known, and Black may well get 2 more points than he should do, which would neutralise any advantage he might get from an one-space-jump.