Sente Vs Gote Which To Play/ Discussion

Table of contents Problem 1 Related problem First example

Table of diagrams White to play and win A white victory White slips Almost Jigo White to play and win Example 1

Questions and comments go here.

Tom:Interesting page Bill! I think it would benefit from having an explicit statement to say that there are no worthwhile plays elsewhere on the board, or tenuki is not an option, or something like that. I guess that is what you mean :)

Bill: Thanks, Tom. :-) I'll edit the intro.

--Funkybside: I have a question; At what (IGS equivilant) rank are players begining to think this deeply about the endgame? (I sure don't do this and can play up to ~3k* IGS players and still have a reasonable chance at winning.) Thanks for any comments.

Bill: For those who may want to do some analysis:

Problem 1

White to play and win  

Enjoy!

A white victory  

I'm very new at endgame analysis, but my 7k mind sees this as best for both players, giving a 1 pt win for White. I can't determine the value of ...I just don't understand miai counting when it comes to sente and gote enough. Anyways 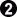is a big gote move, somewhere arond 6 points miai, I think. The outlying stone in the formation confuses the count a bit, though, and eventually requires 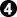. 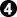is a 4.5 point gote, a 1 point gote, and a .5 gote. W gets tedomari, and wins by 1 point.

White slips  

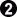If W plays first, B gets to first, and the result comes up jigo.

I wish I could analyse these situations better than this. Can someone help me out with the exact values of and 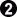in the first diagram? Thanks! ~Alex Baxter

Bill: Thanks for jumping in, Alex. :-)

Almost  

You got the main idea right, but missed a minor detail. is a mistake.

Jigo  

Black can throw in with 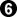, taking away a potential White liberty, and then White must protect with . Result: Jigo.

must be at , which is a double sente at that point.

One nice thing about more realistic problems: They can easily have more than one point. :-)

I'll work out the values of plays later.

[edit]

Related problem

White to play and win  

First example

Example 1  

Here we have a 1 point gote vs. a 1 point sente. What is best play in the corner by each player?

Chris Hayashida: Isn't this wrong? Isn't it a two-point gote play for both sides? I didn't want to edit the page, as my yose is notoriously bad.

Bill: I used miai counting, since that is what to use when comparing sente and gote plays. (You avoid all that multiply or divide by 2 talk.) I guess I should specify miai counting. Thanks. :-)

Tderz: I have problems understanding this:

a) This outcome reminds me of physical/chemical experiments in high school or university. The student measures temperatures of a hot solution of previously dissolved crystals or the magnetic field strength in dependence of distance. S/he finds a dimple in the curve or a different dependency than expected (d2 or d3?), cannot explain it, concludes/states "measuring error!" and simply scrapes of the whole effect (purpose for the whole teaching experiment) by smoothing the measured curve.

Is this as bad as fraud with invented effects? Yes, but less intelligently. It takes energy to think and bravery ("cold fusion") to talk about the possibility of an effect.

Back to the example 1: My first conclusion - not intelligent, not brave - would be that the 1 point gote vs. a 1 point sente are not of the same size, because the result win vs. jigo shows so.

Bill: In this example, White to play prefers to play in the sente first, while Black to play prefers to play in the gote first. You cannot say that one is larger or smaller than the other in an absolute sense.

Miai values reduce the size of the plays to numbers, and do not support such fine distictions. They provide a good guide, though, and the largest play (the one with the largest miai value) is normally the best play.

Despite that both 1 stone can be saved (= 2 points; I am used to a different counting), the lower one has one possible black area point a attached (= conclusion). Hence 2 points ≠ 2+1 = 3 points. (This calculation could be refined if there are more of those stones/rows with different possible area points, e.g. goproblems #3104).

Bill: The plays in that problem are all numbers of different sizes. Simply lengthening the corridors with this type of play does not change the size of the plays. See infinitesimals and related pages.

b) Is this an exception to making the biggest play among two options? I don't think so.

Bill: No, and it does not claim to be. Since the plays are the same size, though, that heuristic does not help. Understanding this example helps, I think, in understanding the more complex ones, where the sizes are different and there are more plays on the board.

It cannot be compared with (urgent plays before big plays where still hundreds of moves might follow. Perhaps I misunderstood all, and this example here should tell me: "Please reflect before you simply count anything what's sente as double in comparison to gote plays - it might not be true." Even then sente play 2x(2+1)=2x3=6 would be > 1 gote play anyway (to teach this, the gote play should have a value of 7 points).

c) How can this be an example of tedomari ( getting the last play)? In this endgame with 2 plays only, the one who starts will simply not get the last play! (if neither player is passing).

Bill: Actually, with correct play the first player also plays last. That is shown on the /parent page.