Kokiri/yose investigation

Consider a Go game where the remaining moves are gote moves without followups. Take the score if white takes all the points to be 0. The remaining moves are {a,b,c,d,,,} listed in decreasing order (a>b>c). It can be considered > not >= because all pairs of equal sized moves can be cancelled out.

Then the score if black takes all the points is a+b+c... so the max score = sum(a,b,c,,,) and min score =0 so the average score is (a+b+c+...)/2.

if black moves first, he takes a, the biggest point, white takes b, the next biggest etc. The score to black is therefore a+c+e... The difference between this and the average is (a+c+e+g)-(a+b+c+...)/2 = (a-b+c-d+...)/2

Thus the value of the first move in a game with pure gote moves w/out followups is (a-b+c-d+e...)/2

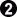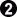Define G to be a set {,,,,} of integers s.t. >>... and consider that they represent a set of moves, as above, but for simplicity, if a move is an n point move then will be n/2

eg this would be a 12 point move, counts as 6  

This game degenerates into the stacks of coins model whereby the net score to black (plays first), g,

  g=-+-...+/-

Case study  

There are 4 moves, {6,5,4,1} so the average score is (6+5+4+1)/2=8 then G as above is {3,2.5,2,.5} ang g=3-2.5+2-.5=2 so the net increase in going first should be 2 points, and since white has 8 points more safe territory than black, black should win by 2 points going first:

Case study  

black score:`12 points white score: 10 points

Consider next a move such as:

Move with a followup for black  

The scores of this move appear to be:

    B <- a -> W
        / \
       b  -6
      / \
     7   1

Then compare this to a simple move as above worth x points to whoever takes it.

• If black takes x, white a, net score x-6.
• If black takes a, white b, black x; score = x+1
• If black takes a, white x, black b; score = 7 -x