Directed Graph Tie Breaking

Directed Graph Tie Breaking is a way of breaking ties among players through graph theory.

In theory, we often assume that go strength is transitive. That if player A is stronger than player B, and player B is stronger than player C, that that automatically means that player A is stronger than player C. Formulaic:

If A > B and B > C then A > C

When players play, the result of the game is an indication of which of them is stronger. If we have the results of a set of games between players (such as in a tournament), then we might write them down as a directed graph, where every player is a node (or vertex) in the graph, and where there is a directed edge between players who have played, pointing from the winner to the loser.

Ideally, this graph would be acyclic. If player A won against B, then there should not be any path in the graph leading from B back to A. If this is the case, then we could use it to rank A above B in the tournament result.

This method can also be used for subsets of the complete set of players. If we have a primary placement criteria, such as a player's score, then we could use graph theory within the subsets of players that are tied.

Consider the following subset of players, with results indicated by arrows:

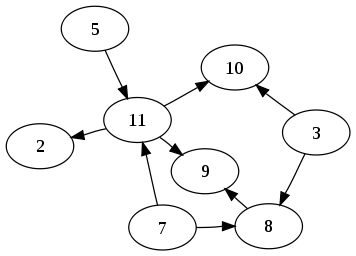
These players might be tied, for example at a 3/5 score. The players that have no losses within the group (3, 5 and 7) might have taken two losses against player in a higher score bracket, while those with two losses within the group (8, 9, 10 and 11) have not played against those in the stronger bracket but have taken their wins against players in a lower bracket. (Or it might be the other way round.)

We can reorder the graph as follows:

Now, we can see that the graph is acyclic, and we can order the group into levels, with any player that has lost to another player being in a lower level than that player. This way, we have partially broken the tie, subdividing the group into three subgroups. From there, another tie breaker could be applied.

This theory is the basis of the Direct Confrontation tie breaker.

Bass: Setting aside all my usual gripes about emphasizing an arbitrary part of the players' performance, I do not think the example graph itself contains any evidence for placing 8 above 10 (or above 2, for that matter.) This is because 11 and 8 are not necessarily on the same level, they are just both below 7.

Herman: Yes, you're right. I was trying to show how Direct Confrontation works, but this example isn't working

Bob McGuigan: One problem is that there is no clear definition of "stronger". Also, it can easily happen that, among three players, A beats B, B beats C, and C beats A. In other words there can be cycles in the directed graph.

Herman: Stronger can be defined pretty well as: "Player A is stronger than Player B if A is more likely to win a game against B than vice versa".

Velobici: Herman presented this method as a tie breaker. Meaning we have reason to believe that this group of players are close in playing strength to each other due to all of them having the same score. With the information, game results in the tournament, that is available to us, we can use the directed acyclic graph to create levels as Herman showed. 8 is above 10 and 2 because 8 has one win and one loss within the group. 10 and 2 have no wins and two losses within the group. This is the reason to place 8 above 2 and 10. Of course, the "best" course of action would be to get more information by having folks play more games. See Round Robin.

Bass: Velobici, what you are describing is not the Directed Graph method, but (a variant of) the Direct Comparison method, which admittedly sometimes produces similar results. Graph theory says nothing about the order of nodes that do not have a path from one node to the other, and because there is no path starting at 8, 2 or 10 and ending at another one of them, graph theory does not actually say anything about their relative order. This is why the example diagram is flawed; it makes a statement about the relative order of 8, 2 and 10, while it shouldn't.