Pass fights in Ultimate Go

There are no pass fights in Ultimate Go, at least not in the classic sense (e.g. the AGA example in the Pass fight). The reason is that, unlike a pass, a delay (in Ultimate Go) does not participate in any game ending mechanism. It is true that in correct play the first delay (which will be an ultimate delay) roughly signifies the beginning of the "counting phase", but that phase transition has no official status in Ultimate Go, and game continues as usual (in particular the game "remembers" who delayed first). See more details below.

However, in examples like Molasses Ko the relevant property of a pass is that it does not change the board position, and this property is shared by a delay. Hence a decisive Mollasses Ko in Ultimate Go will have similar results (i.e. a de-facto no-pass-Go game will ensue).

In detail: in Analysis of Ultimate Go I analyse Fundamental Go (the ruleset we get by omitting Ultimate prisoners from Ultimate Go), and give the definition of current score. The following definition is similar in the Ultimate Go context: assume we're given a ''complete situation'' in an Ultimate Go game, i.e.: (a) whose turn is it; (b) the current board position; (c) the set of previous board positions in the game. We Define the current score to be the "mid-game Komi" needed to make the game a draw. For example, score = +5 means that if Black surrenders now to White's prisoner bowl five of his stones then game should end in a draw (i.e. both players can force a draw); and score = -1 means that if White surrenders to Black's prisoner bowl one stone then game will be drawn (assuming perfect play). It is not hard to show that this integer is well-defined - clearly given enough prisoners a player can force a win (e.g. by simply delaying), and by the nature of the ultimate prisoners device there will be exactly one "mid-game Komi" where both players can force a draw.

Clearly moves by Black can't increase the score, and moves by White can't decrease it. Call a move optimal if it keeps the score unchanged. Note that sometimes there are no optimal moves (so this is not a minimax score) - see Analysis of Ultimate Go. The cost of a move is the amount by which it changes the score. The sente level (of the complete situation) is the cost of a delay. This can be defined even if the player to move has no prisoners, to be the cost of a one-time "reverse delay" (i.e. surrendering a prisoner to the opponent), which certainly equals the cost of a delay (when relevant).

The above definition of score is usually very theoretical, of course, but in the endgame this score can (usually) be computed quite easily, as follows:

Compute for each player a suitable version of the usual "territory" score (i.e. number of territory points plus number of prisoners and dead stones): apply a group tax of 2-points per non-Seki living shape, some Seki false eyes count (see Seki false eye example), prisoners and extra area in Seki count, one-sided dames count, etc. When in doubt you can always play it out fully to see the correct "Ultimate Go scoring" (which is unofficial, i.e. implicit from the ruleset, of course). However, sometimes a complicated inter-connection between "separate" groups might occur, making this "playing out" quite non-trivial and highly context-sensitive - see e.g Superko Example with the SSK variant for a nice example, but of course there are simpler examples of this phenomenon.

Now the score (as defined above) should simply equal Black's "territory score" (again, suitably adjusted) minus White's "territory score".

Now let's go back to the AGA example in Pass fight, and assume the last dame was just filled:

Black to move; no prior ultimate delay; no prisoners (except ultimate prisoners).

 

It's not very hard to see that the Ultimate Go score is -1:

Black's Ultimate-Go-adjusted territory score = 1 ;

White's Ultimate-Go-adjusted territory score = 2.

White's attempt to gain 1 point  

= ultimate delay

= delay (with prisoner )

= resign (since Black's 2 available moves lower the score, i.e. no optimal move)

Black needs just 1 extra prisoner to force a draw:

= delay (with extra prisoner)

= ultimate delay

= declare a draw

Therefore indeed Ultimate Go score = -1.

Efficient perfect play  

= ultimate delay

= resign (and again, Ultimate Go score = -1)

Black's mistake costs him 1 point  

If Black eliminates White's threat with this is actually a mistake, that loses him 1 point:

= ultimate delay

= ultimate delay

= resign

Now Black needs 2 extra prisoners to force a draw, so Ultimate Go score = -2.

For the Tromp-Taylor example in Pass fight we get Ultimate Go score = -17, since the Black "moonshine" group is actually dead. Since there was no Komi the prisoner difference is 2, and we may assume Black has 2 "regular" prisoners (i.e. apart from her ultimate prisoner), and White has 0 regular prisoners.

White to move, last dame just filled, no prior ultimate delay  

Optimal play  

= ultimate delay

= = delay (Black has 2 "regular" prisoners)

= delay (with )

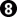= ultimate delay

= delay (with the prisoner captured by )

= resign (since her 2 available moves lower the score)

Shorter optimal play  

= ultimate delay

= = delay (Black has 2 regular prisoners)

= ultimate delay

= fill the Ko

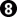= resign (as before, Black needs 17 extra prisoners to force a draw)

Eliminating the "threat" costs 1 point  

As in the AGA example above, if White eliminates the threat (by ) it's actually a "mistake", but a very slight one - the cost of this move (see definition above) is 1 point, i.e. it changes the Ultimate Go score from -17 to -16. Note that the ultimate delay by Black is correct play, since "there's nothing more to achieve", i.e. the sente level (defined above as the cost of a delay) equals 0.

= ultimate delay

= = delay (Black has 2 regular prisoners)

= delay (with the prisoner captured by )

= fill the Ko

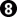= resign (but now Black needs only 16 extra prisoners to force a draw)

Discussion:

1.

2.