Imagist/Problem 5 Solution
The  and
and  groups are in a capturing race. Both groups have four liberties[1] and it is black's turn, so black should be able to win the capturing race.
groups are in a capturing race. Both groups have four liberties[1] and it is black's turn, so black should be able to win the capturing race.
However, if black begins filling outside liberties as normal, he runs into shortage of liberties. If black plays  at
at 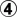 , treating it as a necessary approach move, both groups still have four liberties and it is now white's turn, so black loses.
, treating it as a necessary approach move, both groups still have four liberties and it is now white's turn, so black loses.
If black plays this  and allows white to capture
and allows white to capture  , white must spend another move to capture
, white must spend another move to capture 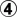 , and the result is not even ko, since black cannot play x due to shortage of liberties.
, and the result is not even ko, since black cannot play x due to shortage of liberties.
 is tesuji-ish, threatening to connect out while reducing a liberty.
is tesuji-ish, threatening to connect out while reducing a liberty. 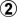 does not gain any liberties, so it is okay that
does not gain any liberties, so it is okay that  reduces liberties for both groups. This is interesting because normally shared liberties should be filled last. Now when white reduces liberties at
reduces liberties for both groups. This is interesting because normally shared liberties should be filled last. Now when white reduces liberties at 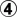 (or white a)
(or white a) 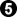 is does not require an approach move at b because it is atari on white's group.
is does not require an approach move at b because it is atari on white's group.
If white plays this 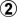 , attempting to connect out, black simply connects himself with
, attempting to connect out, black simply connects himself with  . When white plays
. When white plays 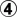 or
or 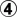 at a,
at a, 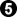 is atari and white doesn't have time to connect.
is atari and white doesn't have time to connect.
It may seem that  and
and  can be switched in the first solution diagram, but
can be switched in the first solution diagram, but  only works because of
only works because of 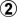 (from the solution diagram). If black reduces a shared liberty first, white simply reduces black's outside liberties and wins.
(from the solution diagram). If black reduces a shared liberty first, white simply reduces black's outside liberties and wins.
Bill: Black can make an approach ko this way. 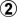 threatens to play at
threatens to play at  , so Black does not have time to connect at
, so Black does not have time to connect at 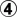 .
.
[1]
![[Diagram]](diagrams/37/f842fa7f46abd3f700cfdae174765402.png)
![[Diagram]](diagrams/32/89ab9f246f0c12b96f2ec458d0cc2a3a.png)
![[Diagram]](diagrams/29/a98ad2623b9a22dab658ced3d9cf23be.png)
![[Diagram]](diagrams/37/db172aaba0d925f03329fc507617228c.png)
![[Diagram]](diagrams/22/a42cd625081e7205d92f668bdae8c245.png)
![[Diagram]](diagrams/47/b51cb49903549e0708600f3bda266751.png)
![[Diagram]](diagrams/19/720c9bb41c68c7bd5de232e54320f876.png)
![[Diagram]](diagrams/41/cce073486ba11c86685a14137af12020.png)
![[Diagram]](diagrams/35/bb858b951ecda3ec533c17f9da4644e9.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)