Stoical Go
In this Go variant, standard ko rules are not used. Instead, it is illegal to make a capture if your opponent made a capture on his previous move.
All other rules are the same as in Go. Suicide of one or more stones is not allowed, and area scoring is used. There is also possible refinement (below) of the basic rule.
All known forced Go cycles are impossible with this rule. The nature of the rule itself suggests that forced cycles are either impossible or astronomically rarer than they are in Go when the superko rule is not used. Ko fights proceed in a similar way to those of Go, with the difference that captures and moves answered by captures aren't valid ko threats. On the other hand, snapbacks are not possible. Under the unrefined rule, it is necessary to make a ko threat before any consecutive capture occurs.
If the board position at the end of your turn is the same as the board position at the end of any of your previous turns, the game ends in a draw. However, if forced cycles are impossible, this will require cooperation between the players, which should not occur in actual play.
Luis Bolaños Mures designed Stoical Go in September 2012. The game is ![[ext]](images/extlink.gif) available to play with the Zillions of Games program. All odd-sized boards from 7x7 to 19x19 are included, as well as the option to use neutral blocking pieces to change the shape of the board.
available to play with the Zillions of Games program. All odd-sized boards from 7x7 to 19x19 are included, as well as the option to use neutral blocking pieces to change the shape of the board.
The designer of Stoical Go recommends playing Incursion Go instead, a more natural variant which preserves snapbacks.
Example
Observations about cycles
Looking for features present in all known forced Go cyclical sequences and then banning moves with one of those features is one of several ways to produce Go-related games without forced cycles. Albeit impractical, the minimally restrictive game produced by this method would consider all those features at once and only forbid those moves that show all of them.
A sample list of such features follows. As new types of cycles are found, the list may be reduced.
This list could also help players to identify potential cycles in the course of a game.
- At least one sequence of two consecutive captures (one by each player) occurs. This is the feature used in Stoical Go.
- At least one sequence of two consecutive incursions (one by each player) occurs. An incursion is a placement in an enemy territory. A territory is a maximal set of orthogonally adjacent empty points. An enemy territory is a territory such that all stones orthogonally adjacent to points in the territory are of your opponent's color. This is the feature used in Incursion Go.
- At least once a capture by one player is immediately followed by an enemy placement inside one of the player's territories. (This feature isn't used in the variants below but produces an interesting variant by itself.)
- No single point occupied by one player at one time is occupied by the other player at any other time. (This feature isn't used in the variants below.)
- No move results in the capture of more than four stones.
- No placement is part of a string bigger than four stones.
- No capturing string is bigger than four stones. A capturing string is the string of a capturing placement, but not the other strings that take part in a capture.
- No capturing domain is bigger than four stones. A capturing domain is the domain of a capturing placement before any removals. A domain of one color is a maximal set of orthogonally adjacent points that are not occupied by stones of the opposite color.
- No placement is part of an estate bigger than four points, even after removals. An estate is a string along with all empty points that, if occupied at once by stones of the string's color, would make the string larger without marging it with other strings of its color.
- No move results in the capture of more than one string.
- No snapback occurs. A snapback is defined as a capture of a single stone by extending an already existing string followed by the capture of said capturing string by placing a stone on the just vacated point, provided that said stone is not in atari as a result.
- No capture with the features of the first capture in a snapback occurs.
- After a capture, more than one friendly string is always adjacent to the area vacated by the capture. Note that this is the same as in captures affected by the basic ko rule.
- At least one capture occurs where all liberties of the capturing string are part of the area vacated by the capture.
- In a capture where all liberties of the capturing string are part of the area vacated by the capture, the capturing string (and domain) and the captured string are always the same size.
- No capture occurs where the capturing string has more than one liberty before any removals.
- When a capturing string has one liberty before any removals, said capturing string is always made of exactly one stone.
- When a capturing string has one liberty before any removals, said liberty is always part of an empty area that isn't adjacent to any other friendly stones. An empty area is a maximal set of orthogonally adjacent empty points.
- All captured strings are open lines of stones. An open line is a set of points such that none of them is adjacent to more than two other points in the set and at least one of them is adjacent to less than two other points in the set.
- All capturing strings and all capturing domains are open lines before removals. A capturing string, again, is the string of a capturing placement.
- All placements are part of open lines of stones.
- All placements are part of estates that are open lines, even after removals.
Variant without the ko rule
Based on these features, a minimally restrictive replacement for the ko rule resulting in a soft finite game where players aren't required to remember more than one bit of information could be formulated as follows:
You can't make a disturbing capture immediately after a disturbing capture by your opponent.
Note that snapbacks are still possible under this rule.
Definitions:
A set is maximal if it's as large as it can be, i.e. if it's not a subset of a larger set of the same type.
A string of one color is a maximal set of orthogonally adjacent stones of that color.
A domain of one color is a maximal set of orthogonally adjacent points that are not occupied by stones of the opposite color.
A capturing string is the string of a capturing placement.
A capturing domain is the domain of a capturing placement before any removals.
An open line is a set of orthogonally adjacent points such that none of them is adjacent to more than two other points in the set and at least one of them is adjacent to less than two other points in the set.
A disturbing capture is a capture of exactly one enemy string such that a) the capturing domain includes exactly one string, b) the captured string and the capturing domain are open lines smaller than five points, and c) the capturing string isn't bigger than the captured string.
Variants with the ko rule
The basic ko rule can be combined with a restriction on the move after two consecutive captures based on the observations above. This method produces games almost indistinguishable from Go without ever requiring players to remember more than two bits of information, apart from the coordinates of the opponent's latest move (required by the ko rule). A few examples of such restrictions follow.
This is the "2-2-2 rule":
If the latest two board plays (with no passes in between) have been captures, your placement must be part of a string with more than two stones (including itself) or more than two liberties after removals (or both).
Even simpler is the "2-2 rule":
If the latest two board plays (with no passes in between) have been captures, your placement must be part of a string with more than two liberties after removals.
Of course, a single stone is also a string.
Also interesting is the "4-point rule":
If the latest two board plays (with no passes in between) have been captures, your placement must be part of an estate bigger than four points after removals.
An estate is a string along with all empty points that, if occupied at once by stones of the string's color, would make the string larger without merging it with other strings of its color.
The "OLE rule" (Open Line Estate rule) has the best subjective chances of preventing all forced cycles, both known and unknown:
If the latest two board plays (with no passes in between) have been captures, your placement must not be part of an estate that is an open line after removals.
As before, an open line is a maximal set of stones such that none of them is adjacent to more than two other stones in the set and at least one of them is adjacent to less than two other stones in the set.
There is no obvious reason why forced cycles involving strings bigger than four stones couldn't exist, but it would make sense that all strings involved in all forced cycles were open lines. (A cycle involves a string if a stone is added to that string in the course of it.)
Discussion
tapir: You are aware that you will have many "right to capture" fights? Even snapbacks are impossible in your variant.
luigi87: Not that many, but yes, often a player will have to use a ko threat in a given sequence to earn the right to capture back. The same happens with snapbacks as well. This feature adds a global positional factor to the evaluation of local fights, which needn't be a bad thing. As for snapbacks, they can be explicitly allowed without reintroducing forced cycles into the game.
willemien: How about Eternal Life?
luigi87: Eternal life is not possible in Stoical Go.  in the entry's example sequence is an immediate re-capture.
in the entry's example sequence is an immediate re-capture.
Sandra: [Cooperative cycle (not a forced cycle):]
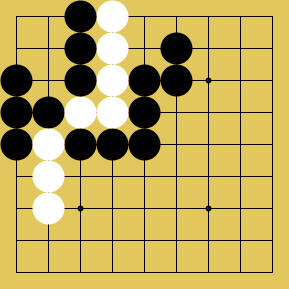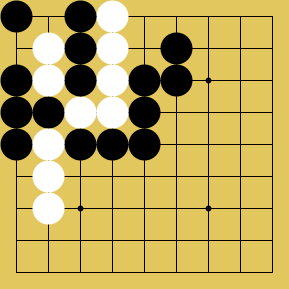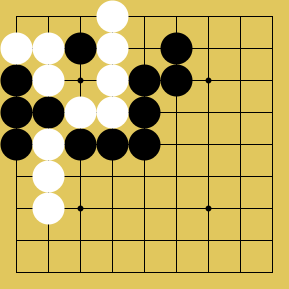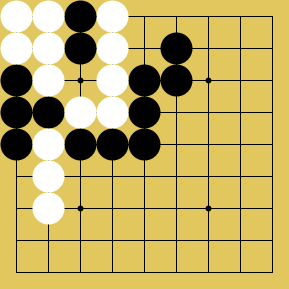
Slarty: It's still (technically) needed to know what happens if a repeating position is played, to define the game. It could be a source of a little confusion though I think the page is clear. (would imagine borrowing chess's threefold repetition = draw in a very thorough description). Anyway, the game should be pretty good. It's difficult to make it the same as Go (in under ten words, at least) - because there can be snapbacks of any size.
A funny variant idea (doesn't need its own page) is to forbid the last player who captured (or the one with the most prisoners) from capturing again. It's sort of like the doubling die mechanic in backgammon.
luigi87: Yes, it reminds me of ![[ext]](images/extlink.gif) a set of bizarre finite Go variants that I discussed a while ago on Life In 19x19. In the most basic one, once a player makes a capture for the first time, that player can’t create any more strings for the rest of the game. It creates an intriguing build up of tension prior to the point when one of the players decides to make a capture. As for repetitions, you're right. I've just added a rule to handle them.
a set of bizarre finite Go variants that I discussed a while ago on Life In 19x19. In the most basic one, once a player makes a capture for the first time, that player can’t create any more strings for the rest of the game. It creates an intriguing build up of tension prior to the point when one of the players decides to make a capture. As for repetitions, you're right. I've just added a rule to handle them.
Slarty: Proposal: if your opponent captured 1 or more stones on their last turn, you may not capture exactly 1 stone if either that stone is your opponent's move or your move is self atari.
luigi87: Eternal life and round robin ko are possible under that rule.
anonymous: This variant is a little similar to one variant related to simultaneouness I was thinking about, that was this: White cant move to a place that had an piece on previous turn and cant capture an piece that was included on previous turn or that make an group with a piece added on previous turn. Game end after 2 consecutive passes if the last pass was a white one, or 3 passes (white pass will still be the last one.
![[Diagram]](diagrams/28/812fe5d33d4ab762cbb03a95d42a6702.png)
![Sensei's Library [Welcome to Sensei's Library!]](images/stone-hello.png)